As sequências numéricas são um conceito fundamental na matemática, com aplicações em várias áreas do conhecimento, como a física, a economia e a informática. Elas permitem-nos compreender padrões, prever comportamentos e descrever fenómenos de forma matemática. Para entender melhor o que é uma sequência numérica e como funciona, começaremos com um exemplo simples.
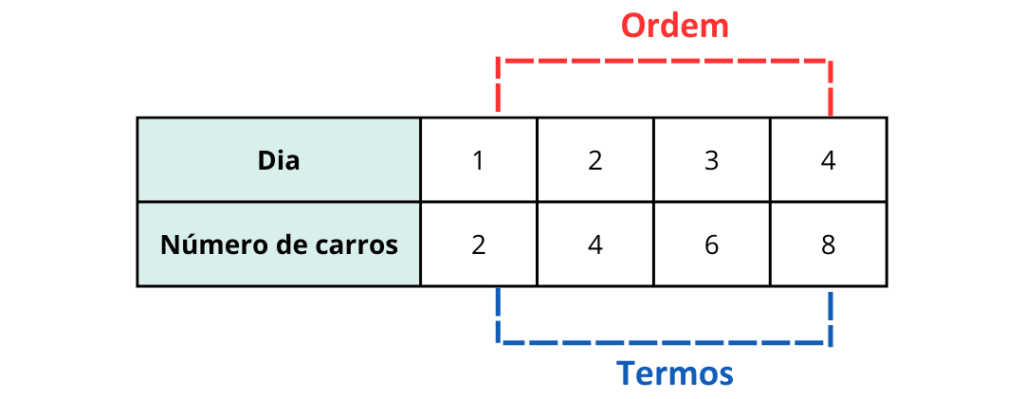
O João gosta de observar o movimento na sua rua através da janela de casa. Recentemente, ele começou a contar quantos carros azuis passam pela rua a cada dia. Ele decidiu registar o número de carros azuis que vê diariamente durante quatro dias. Aqui estão os resultados que ele anotou:

Podemos ver um padrão nos números que o João registou. O número de carros azuis aumenta em 2 a cada dia. Este conjunto de números forma uma sequência numérica.
Os números observados pelo João podem ser descritos como:
2,4,6,8
Uma sequência numérica é uma lista ordenada e finita de números. Quando esta sequência tem um número infinito de números passa a chamar-se de sucessão.
Cada número na sequência é chamado de termo e podemos identificar um termo específico pela sua posição na sequência, conhecida como a ordem do termo.
Uma das formas mais importantes de descrever uma sequência é através de uma fórmula que permite calcular qualquer termo da sequência. Essa fórmula é conhecida como termo geral da sequência.
Voltando ao exemplo dos carros azuis e prolongando a sequência, mantendo a regularidade até à ordem n, temos:
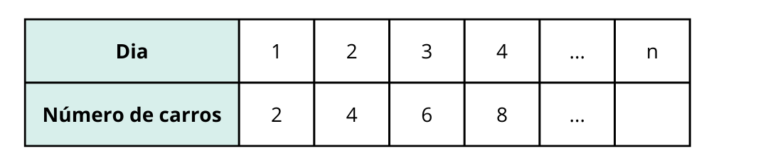
Observamos que cada termo é obtido multiplicando a posição n por 2.

Assim, o termo geral pode ser expresso como: 2n
Com esta fórmula, podemos calcular qualquer termo da sequência. Por exemplo, para encontrar o número de carros azuis que o João verá no 5º dia, basta substituir n por 5: 2\times 5=10 \ carros
Então, e se na rua do João tivessem passado 18 carros azuis, qual seria o dia?
Para descobrir isso, podemos usar a fórmula do termo geral e resolver a equação para n.
Basta igualar o termo geral a 18: 2n=18\Leftrightarrow n=\frac{18}{2}=9
Portanto, se tivessem passado 18 carros azuis, isso teria ocorrido no 9.º dia.
As sequências numéricas são ferramentas poderosas para entender padrões e regularidades. São definidas por termos ordenados, onde cada termo tem uma posição (ordem) e pode ser calculado usando uma fórmula conhecida como termo geral. Além disso, é possível fazer o processo inverso, para descobrir a ordem de um termo específico dentro da sequência. Ao compreender como funcionam, podemos aplicá-las em várias áreas para resolver problemas complexos e descrever fenómenos de maneira precisa.