Desde os primórdios da civilização, o ser humano sentiu a necessidade de contar e quantificar o mundo ao seu redor. Esta necessidade levou à criação dos números naturais, um conjunto que utilizamos diariamente para enumerar objetos, marcar datas e medir quantidades.
Por exemplo, ao contar o número de fatias de pizza num prato, usamos os números naturais: uma, duas, três ou até mesmo nenhuma (zero). Este conjunto de números é representado pelo símbolo \mathbb{N}:
\mathbb{N}=\left\{0,1,2,3… \right\}
No entanto, os números naturais não são suficientes para quantificar tudo o que nos rodeia. Por exemplo, pensaremos nas temperaturas que atingem em Portugal. O normal é termos temperaturas positivas, por exemplo 12ºC e 16ºC. Por outro lado, nos dias mais frios, é possível atingir os 0ºC ou até mesmo temperaturas negativas, como é o caso de -1 e do -2.
Uma vez que os números representados não têm casas decimais, dizemos que são números inteiros.

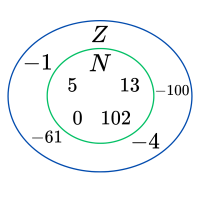
É o conjunto formado pelos números inteiros negativos, inteiros positivos e pelo zero, e representa-se pela letra \mathbb{Z} .
\mathbb{Z}=\left\{…,-3,-2,-1,0,1,2,3… \right\}
Podemos ainda considerar outros subconjuntos do conjunto \mathbb{Z}:
\mathbb{Z}^{-}=\left\{…,-3,-2,-1 \right\}\to conjunto dos inteiros negativos
\mathbb{Z}_{0}^{-}=\left\{…,-3,-2,-1,0 \right\}\to conjunto dos inteiros não positivos
\mathbb{Z}^{+}=\left\{1,2,3,… \right\}\to conjunto dos inteiros positivos
\mathbb{Z}_{0}^{+}=\left\{0,1,2,3,… \right\}\to conjunto dos inteiros não negativos =\mathbb{N}
Muitas vezes, é útil representarmos os números numa reta chamada reta numérica.

O valor absoluto, ou módulo, é a distância do ponto que o representa na reta numérica à origem. Por exemplo, considera o ponto A na reta numérica abaixo.

A distância do ponto à origem é de duas unidades. Por outras palavras diz-se que o valor absoluto de 2 é 2 , e escreve-se |2|=2.
Observa agora o ponto B.

O ponto B está também a duas unidades de distância da origem. Logo o seu valor absoluto é igualmente 2, ou seja,|-2|=2.
Repara que os pontos A e B têm o mesmo valor absoluto. Quando isso acontece, diz-se que os dois números são simétricos. Ou seja:
Por outras palavras, o simétrico de um número é o mesmo número, mas com sinal contrário.
Dados dois números, é maior o que se encontrar mais à direita na reta numérica. Por exemplo:

Repara que se ambos forem negativos, é maior o que tiver menor valor absoluto. (mais próximo do zero!)
Na adição e subtração de dois números inteiros:
+2+3=+5

-1-3=-4

+4-1=+3
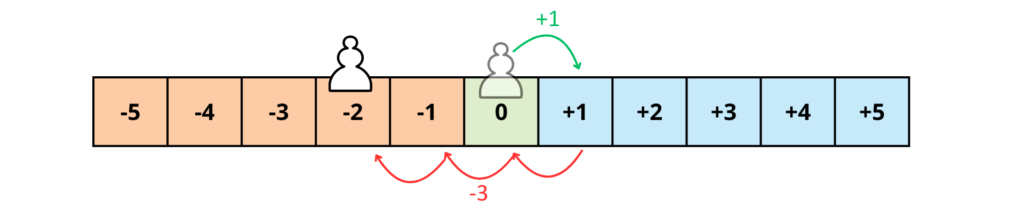
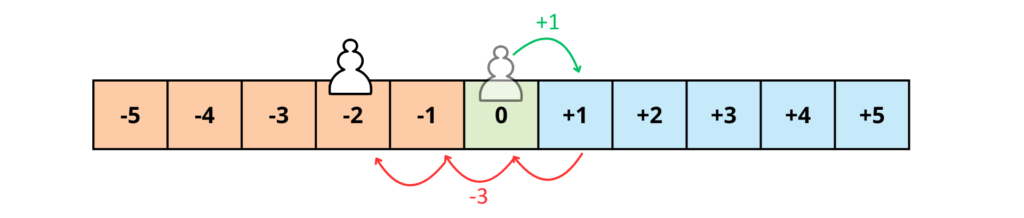
+1-3=-2
Expressões numéricas com parênteses
Para simplificar uma expressão numérica com parênteses, pode-se utilizar as seguintes regras:
Compreendemos agora como os números naturais e inteiros se interligam, formando a base da aritmética e permitindo operações como adição e subtração. Estes conceitos preparam-nos para um próximo passo essencial: os números racionais.