Raiz quadrada e cúbica
Raiz Quadrada
Introdução à raiz quadrada
Observa a sequência de quadrados e as suas respetivas áreas e comprimentos de lado.
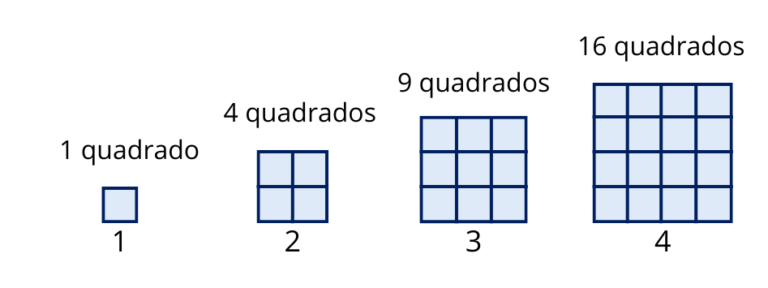
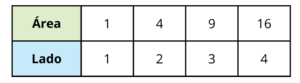
Na tabela, cada quadrado tem um lado inteiro e a sua área é calculada como o lado multiplicado por si mesmo, ou seja, o lado ao quadrado.
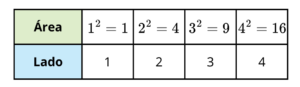
Conceito de Raiz Quadrada
Observando a tabela, percebemos que para cada área de um quadrado existe um comprimento específico do lado que, ao ser elevado ao quadrado, resulta nessa área. A raiz quadrada é justamente a operação inversa de elevar ao quadrado: ela permite encontrar o valor do lado a partir da área de um quadrado.
Assim, se conhecemos a área de um quadrado, por exemplo, 25, a raiz quadrada dessa área nos dá o comprimento do lado, que é 5 (\sqrt{25}=5).
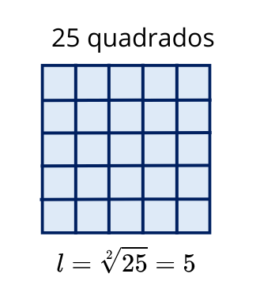
Exemplos e Quadrados Perfeitos
Vamos ver mais alguns exemplos que ilustram essa ideia:
- A raiz quadrada de 9 é 3, pois 3^{2}=9 \to \sqrt{9}=3
- A raiz quadrada de 49 é 7, pois 7^{2}=49 \to \sqrt{49}=7
- A raiz quadrada de 100 é 10, pois 10^{2}=100 \to \sqrt{100}=10
Esses exemplos ilustram o conceito de quadrados perfeitos — números cuja raiz é um número natural.
Entender a raiz quadrada como o inverso de elevar ao quadrado é essencial para resolver muitos problemas matemáticos e facilita o cálculo de comprimentos, áreas e outras medidas em contextos práticos e teóricos.

Raiz Cúbica
Introdução
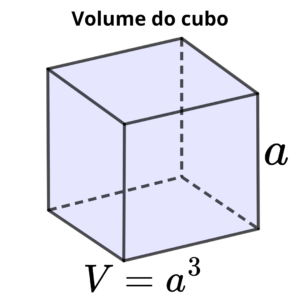
Assim como a raiz quadrada “desfaz” a operação de elevar ao quadrado, a raiz cúbica é o inverso de elevar ao cubo.
A raiz cúbica de um número, então, representa o valor que, elevado ao cubo, resulta nesse número. É indicada pelo símbolo \sqrt[3]{}.
Exemplos Visuais de Raiz Cúbica
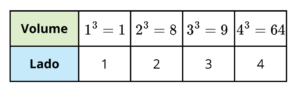
Para ilustrar, vejamos uma tabela com volumes de cubos e o comprimento do seu lado correspondente. Cada volume resulta da operação de elevação ao cubo, e a raiz cúbica nos permite obter o comprimento do lado a partir desse volume.
Exemplos e Cubos Perfeitos
Tal como ocorre com a raiz quadrada e os quadrados perfeitos, a raiz cúbica é mais simples de calcular para números que são cubos perfeitos, ou seja, números que resultam de um número inteiro multiplicado por si mesmo três vezes. Por exemplo:
- A raiz cúbica de 8 é 2, pois 2^{3}=8 \to \sqrt[3]{8}=2
- A raiz cúbica de 27 é 3, pois 3^{3}=27 \to \sqrt[3]{27}=3
- A raiz cúbica de 125 é 5, pois 5^{3}=125 \to \sqrt[3]{125}=5
Esses exemplos mostram como a raiz cúbica pode ser usada para encontrar valores exatos de lado em figuras tridimensionais, facilitando cálculos de volume.