Introdução
O Vasco esqueceu-se do código do seu cacifo. Para não pedir à auxiliar da escola que o arrombe, decidiu tentar por tentativa e erro. Sabendo que o código é um número com três algarismos, quantas combinações possíveis ele pode tentar?
Resolução:
Cada algarismo do código pode ser qualquer número de 0 a 9, ou seja, há 10 possibilidades para cada posição.
Assim, o número total de combinações possíveis é dado por:
$$10\times10\times10$$
Ou, utilizando potências:
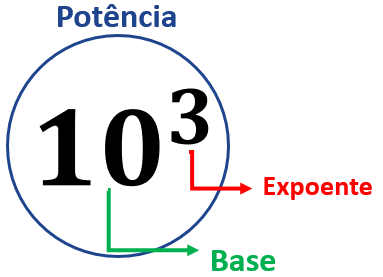
$$10^{3}=10\times10\times10=1000$$
Aqui, o número 10 é a base e 3 é o expoente. A base é o número que estamos a multiplicar por ele mesmo, e o expoente indica quantas vezes isso é feito.
$$\left( -2 \right)^{3}=(-2)\times(-2)\times(-2)=8$$
$$\left( \frac{2}{3} \right)^{3}=\frac{2^{3}}{3^{3}}=\frac{2\times2\times2}{3\times3\times3}=\frac{8}{27}$$
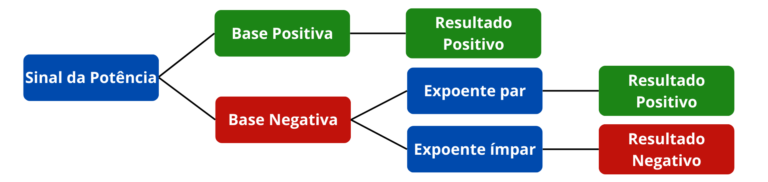
Sinal de uma potência de base racional e expoente inteiro positivo.
- Potências com base positiva
- Potências com base negativa
Em conclusão:
Operações com potências de expoente inteiro
Quando trabalhamos com potências, existem regras que nos ajudam a simplificar cálculos, especialmente em casos onde as potências têm bases ou expoentes iguais. Estas propriedades são essenciais para manipular expressões de forma eficiente.
- Multiplicação de potências com a mesma base: Dá-se a mesma base e somam-se os expoentes.
- Divisão de potências com a mesma base: Dá-se a mesma base e subtrai-se os expoentes.
- Multiplicação de potências com o mesmo expoente: Mantém-se o expoente e multiplicam-se as bases.
- Divisão de potências com o mesmo expoente: Mantém-se o expoente e divide-se as bases.
- Potência de uma potência: Multiplicam-se os expoentes.
- Potência de expoente zero: Qualquer base diferente de zero elevada a zero é igual a 1.
- Potência de expoente negativo: Inverte-se a base e troca-se o sinal do expoente.
