No 7.º ano, já te familiarizaste com os números racionais (Q), que são aqueles que podem ser representados por uma fração onde tanto o numerador como o denominador são números inteiros. Aprendeste também a somar e subtrair esses números de forma eficaz.
Neste artigo, vamos aprofundar o estudo dos números racionais, explorando não só a sua representação na forma de fração, mas também na forma de dízima.
Exemplo:
Vamos considerar a quantidade de pizza disponível em cada fatia.
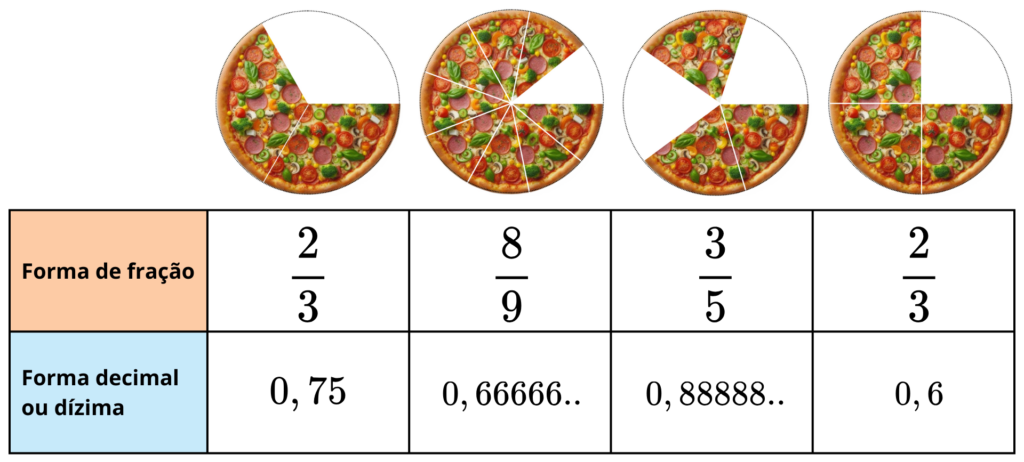
Como podes observar, a quantidade de pizza pode estar representada na forma de fração, mas também na forma decimal ou dízima.
Exemplos:
\bullet \space 0,4=\frac{4}{10}=\frac{2}{5}\qquad\bullet \space 0,61=\frac{61}{100}
Exemplos:
\bullet \space \frac{8}{9}=0,888(8)\qquad\bullet \space \frac{1}{6}=0,1666(6)
Em conclusão, qualquer número racional pode ser representado por uma dízima finita ou por uma dízima infinita periódica.
Multiplicar números racionais é um processo simples e direto, que segue as mesmas regras da multiplicação de frações. Para multiplicar dois números racionais, basta multiplicar os numeradores entre si e os denominadores entre si. O resultado é uma nova fração que também é um número racional.
Regra geral:
\frac{a}{b}\times\frac{c}{d}=\frac{a\times c}{b\times d}
Exemplo 1:
\frac{2}{3}\times\frac{4}{5}=\frac{2\times 4}{3\times 5}=\frac{8}{15}
Exemplo 2:
-\frac{3}{7}\times\frac{5}{2}=-\frac{3\times 5}{7\times 2}=-\frac{15}{14}

A divisão de números racionais segue uma regra importante: dividir por uma fração é o mesmo que multiplicar pelo inverso dessa fração.
O inverso de uma fração \frac{c}{d} é \frac{d}{c}.
Regra geral:
\frac{a}{b}\div \frac{c}{d}=\frac{a}{b}\times \frac{d}{c}=\frac{a\times d}{b\times c}
Exemplo 3:
\frac{3}{4}\div \frac{2}{5}=\frac{3}{4}\times \frac{5}{2}=\frac{3\times 5}{4\times 2}=\frac{15}{8}
Exemplo 4:
-\frac{7}{9}\div \frac{2}{3}=-\frac{7}{9}\times \frac{3}{2}=-\frac{7\times 3}{9\times 2}=-\frac{21}{18}=-\frac{7}{6}\text{( após simplificação)}