No artigo anterior viu-se que dois polígonos são semelhantes quando os comprimentos dos lados correspondentes são diretamente proporcionais e os ângulos internos correspondentes são iguais.
Contudo, nem sempre teremos informações sobre todos os lados ou sobre todos os ângulos! Neste artigo, exploraremos como, no caso dos triângulos, é possível determinar a semelhança usando apenas alguns lados e ângulos.
No caso dos triângulos, estudaremos três critérios que nos permitem averiguar se dois triângulos são semelhantes:
Dois triângulos são semelhantes quando os comprimentos dos lados correspondentes são diretamente proporcionais aos comprimentos dos lados correspondentes do outro.
Exemplo 1
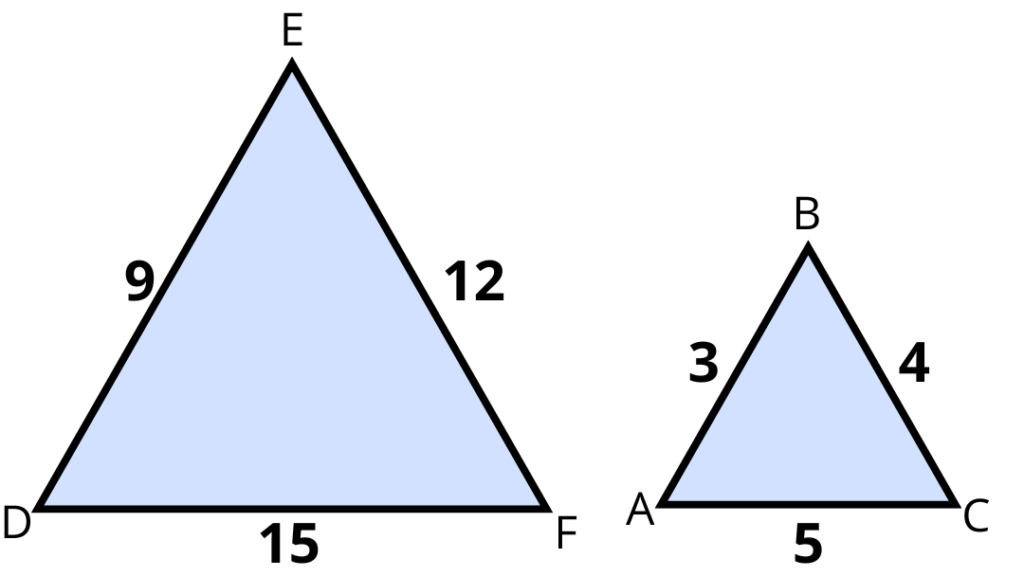
\frac{\overline{DE}}{\overline{AB}}=\frac{\overline{EF}}{\overline{BC}}=\frac{\overline{DF}}{\overline{CA}}=3
Os comprimentos dos três lados são diretamente proporcionais, logo, pelo critério LLL, os triângulos são semelhantes.
Dois triângulos são semelhantes quando dois ângulos internos de um são iguais a dois dos ângulos internos do outro.
Exemplo 2
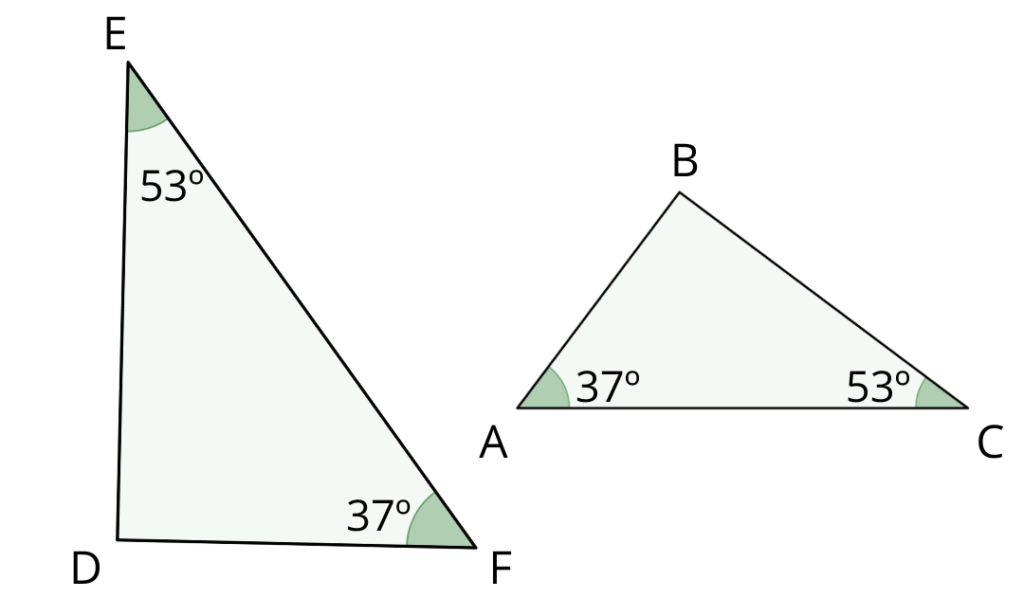
D\hat{E}F=B\hat{C}A
D\hat{F}E=B\hat{A}C
Logo, pelo critério AA, os triângulos são semelhantes.
Dois triângulos são semelhantes quando os comprimentos de dois lados são diretamente proporcionais e o ângulo por eles formado são iguais.
Exemplo
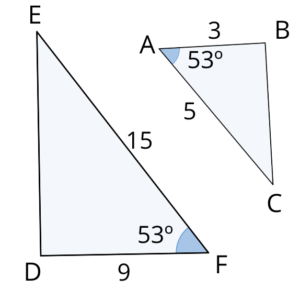
\frac{\overline{EF}}{\overline{AC}}=\frac{\overline{DF}}{\overline{AB}}=3
E\hat{F}D=C\hat{A}B
Logo, pelo critério LAL, os triângulos são semelhantes.