Em Matemática diz-se que duas figuras são semelhantes se possuírem a mesma forma, podendo ou não ser do mesmo tamanho.
Tal como ilustra o esquema seguinte, é possível obter figuras semelhantes quando aumentamos, diminuirmos ou mantemos o tamanho de uma figura (mantendo a sua forma).
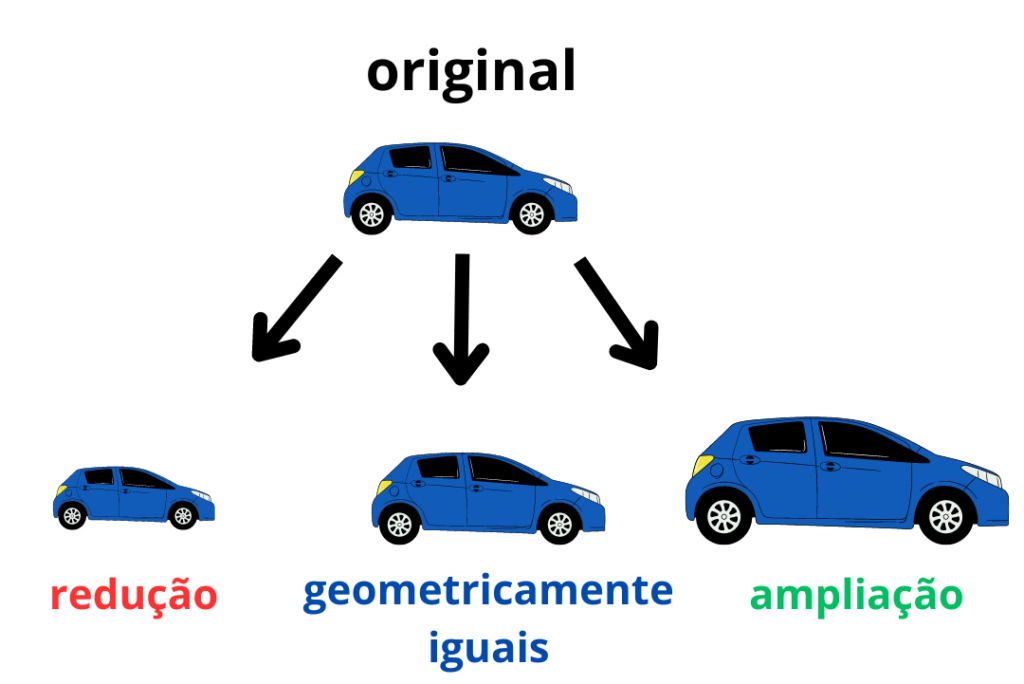
Dois polígonos são semelhantes quando:
Exemplo 1
Averiguemos se os dois polígonos são semelhantes.
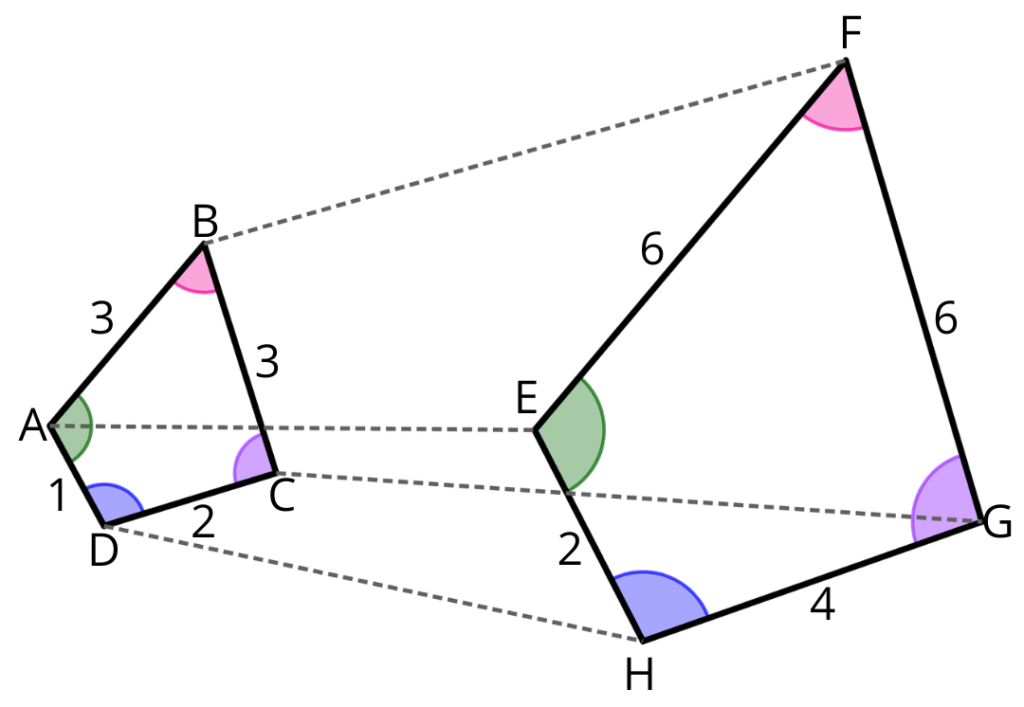
Primeiro, é necessário saber identificar os elementos correspondentes:
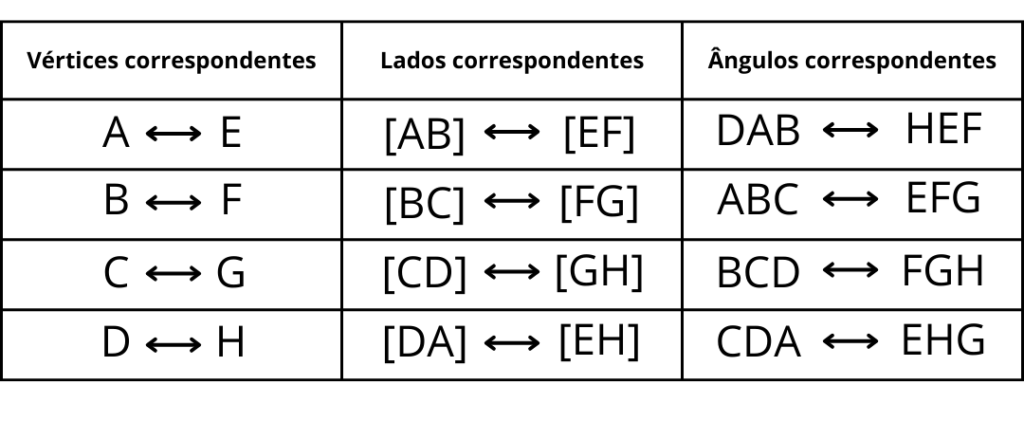
Pela figura verifica-se que:
D\hat{A}B = H\hat{E}F
A\hat{B}C = E\hat{F}G
B\hat{C}D = F\hat{G}H
C\hat{D}A = E\hat{H}G
Logo os ângulos internos correspondentes são iguais.
\frac{\overline{EF}}{\overline{AB}}=\frac{\overline{FG}}{\overline{BC}}=\frac{\overline{CD}}{\overline{GH}}=\frac{\overline{DA}}{\overline{EH}}=2
Como os ângulos correspondentes são iguais e os lados correspondentes são diretamente proporcionais, os polígonos [ABCD] e [EFGH] são semelhantes.
À constante de proporcionalidade, que neste caso é 2, chama-se razão de semelhança.
Se a razão de semelhança é:
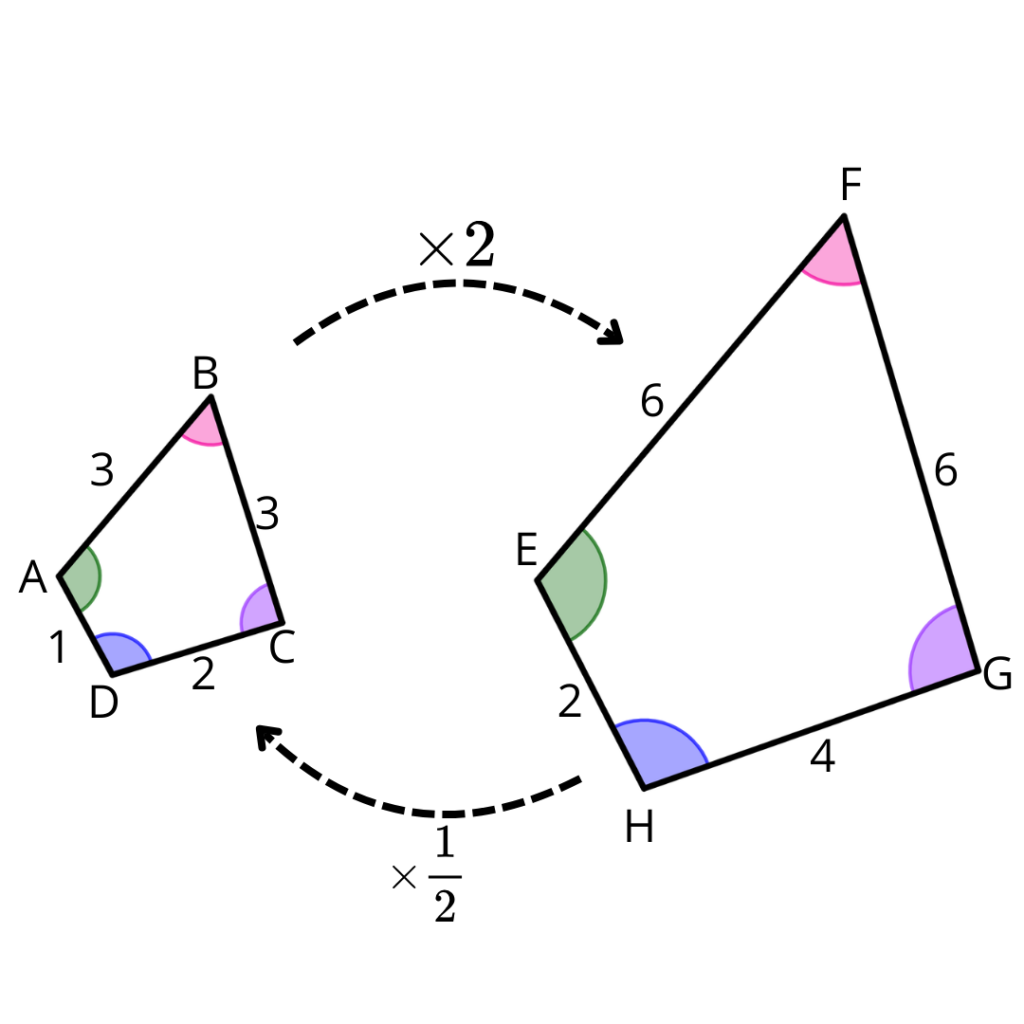
Seja r a razão de semelhança que transforma uma figura original na sua transformada, tem-se as seguintes relações:
A razão de semelhança: \frac{\text{Lado transformado}}{\text{Lado original}}=r
A razão entre os perímetros é: \frac{\text{Perímetro transformado}}{\text{Perímetro original}}=r
A razão entre as áreas é: \frac{\text{Área transformado}}{\text{Área original}}=r^{2}
Exemplo 2
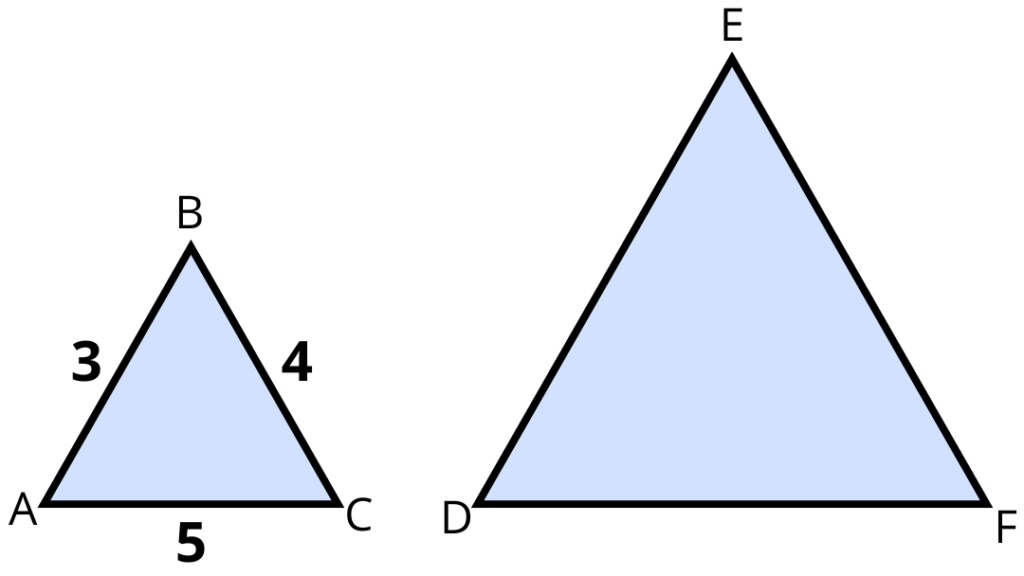
Considera os dois polígonos semelhantes, sendo 2 a razão de semelhança que transforma [ABC] em [DEF]. Sabe-se que ([ABC]\) tem 12 \text{cm} de perímetro e 6 \text{cm}^{2} de área.
– Perímetro
Uma vez que a razão entre os perímetros é dada pela expressão:
\frac{\text{Perímetro transformado}}{\text{Perímetro original}}=r
Substituindo os dados tem-se:
\frac{\text{Perímetro transformado}}{\text{12}}=2\Leftrightarrow \text{Perímetro transformado}=2\times12=24 \text{ cm}
– Áreas
Uma vez que a razão entre as áreas é dada pela expressão:
\frac{\text{Área transformado}}{\text{Área original}}=r^{2}
Substituindo os dados tem-se:
\frac{\text{Área transformado}}{\text{6}}=2^{2}\Leftrightarrow \text{Área transformado}=4\times6=24 \text{ cm}^{2}