A proporcionalidade direta é um conceito matemático que encontramos frequentemente no nosso dia-a-dia. É uma relação simples onde duas grandezas crescem ou diminuem na mesma proporção. Para compreender este conceito de forma clara, vamos analisar um exemplo prático e comum: a preparação de panquecas.
A Teresa adora fazer panquecas ao fim de semana e tem uma receita que utiliza a seguinte proporção: 4 chávenas de farinha para cada 2 ovos. Esta proporção é fundamental para que as panquecas fiquem com a consistência perfeita.
Pergunta: O que acontece se a Teresa quiser dobrar a receita? Ou fazer um quarto da receita?
Vamos explorar as respostas para estas perguntas.
Análise da Receita
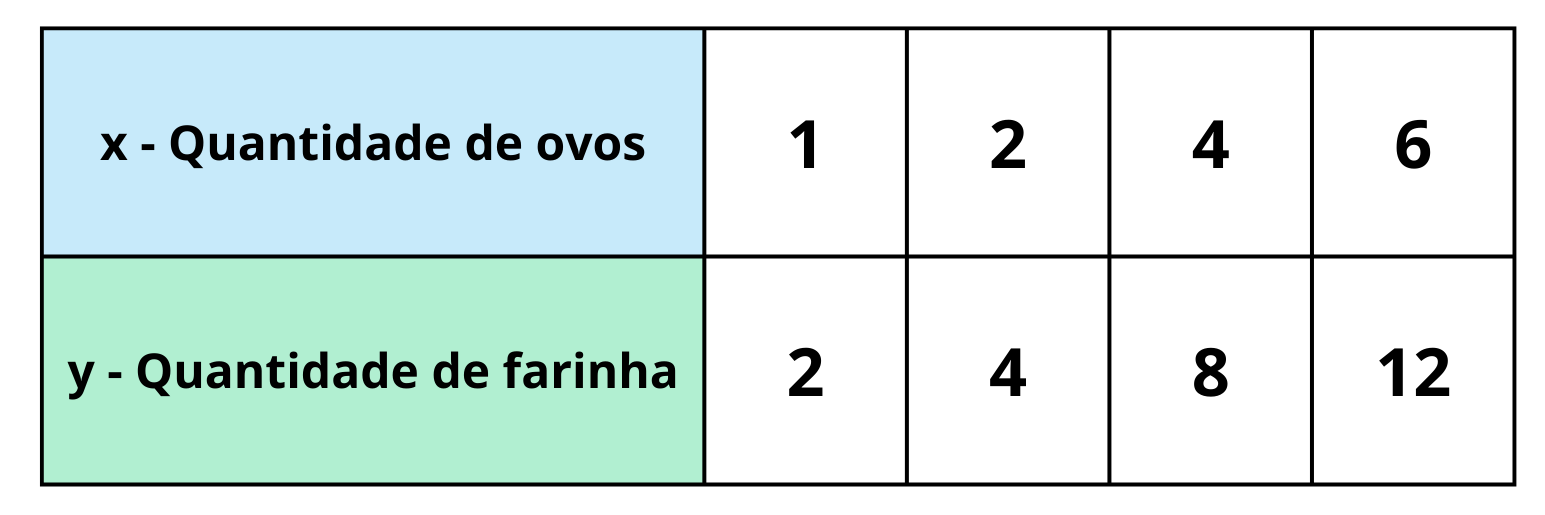
Para perceber como a quantidade de farinha e o número de ovos se relacionam, vejamos algumas situações:

Aqui podemos observar uma relação: ao multiplicar ou dividir a quantidade de farinha, multiplicamos ou dividimos também o número de ovos pela mesma quantidade. A relação entre as duas grandezas (quantidade de farinha e ovos) é sempre a mesma.
Com base no exemplo acima, podemos definir a proporcionalidade direta da seguinte forma:
Definição:
Uma grandeza Y diz-se diretamente proporcional a outra grandeza X quando a razão entre os valores da primeira (y) e os valores correspondentes da segunda (x) é constante. A este valor constante dá-se o nome de constante de proporcionalidade direta.
No exemplo das panquecas, temos:
\frac{y}{x}=\frac{2}{1}=\frac{4}{2}=\frac{8}{4}=\frac{12}{6}=2
constante de proporcionalidade
Depois de fazer tantas panquecas deliciosas, a Teresa decidiu começar a vendê-las. Ela definiu que cada panqueca custará 2,5€.
Considera a tabela que relaciona o “número de panquecas” e o “preço”.
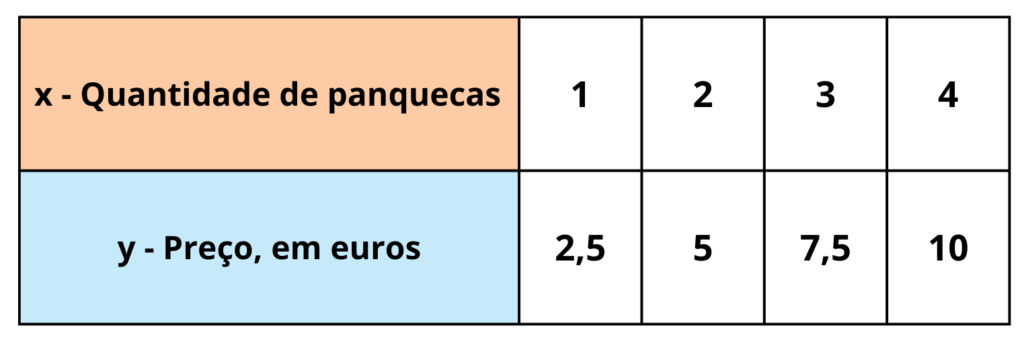
Como \frac{y}{x}=\frac{2,5}{1}=\frac{5}{2}=\frac{7,5}{3}=\frac{10}{4}=2,5 as duas grandezas são diretamente proporcionais, sendo 2,5 a constante de proporcionalidade.
Nota também que, para cada número de panquecas (x), corresponde um único valor do preço total (y). Assim, podemos dizer que esta relação é uma função, pois a cada valor de x corresponde um único valor de y.
Este tipo de função, onde uma grandeza é diretamente proporcional a outra, é chamada de função de proporcionalidade direta. É representada por uma expressão da forma: y=\frac{k}{x} onde:
No caso da Teresa, a constante de proporcionalidade direta k é 2,5, pois cada panqueca custa 2,5€. Portanto, a função que relaciona o número de panquecas com o preço total é:
f(x)=2,5x
Significado da Constante de Proporcionalidade
A constante de proporcionalidade k tem um significado claro no contexto do exemplo da Teresa: é o preço de uma única panqueca. A constante k=2,5 significa que, para cada unidade de panquecas adicionais que a Teresa vender, o preço total aumentará em 2,5€.
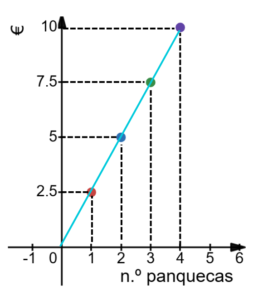
Gráfico da Função
O gráfico de uma função de proporcionalidade direta é sempre uma linha reta que passa pela origem do referencial.
O gráfico que representa a função do exemplo é o da figura seguinte: