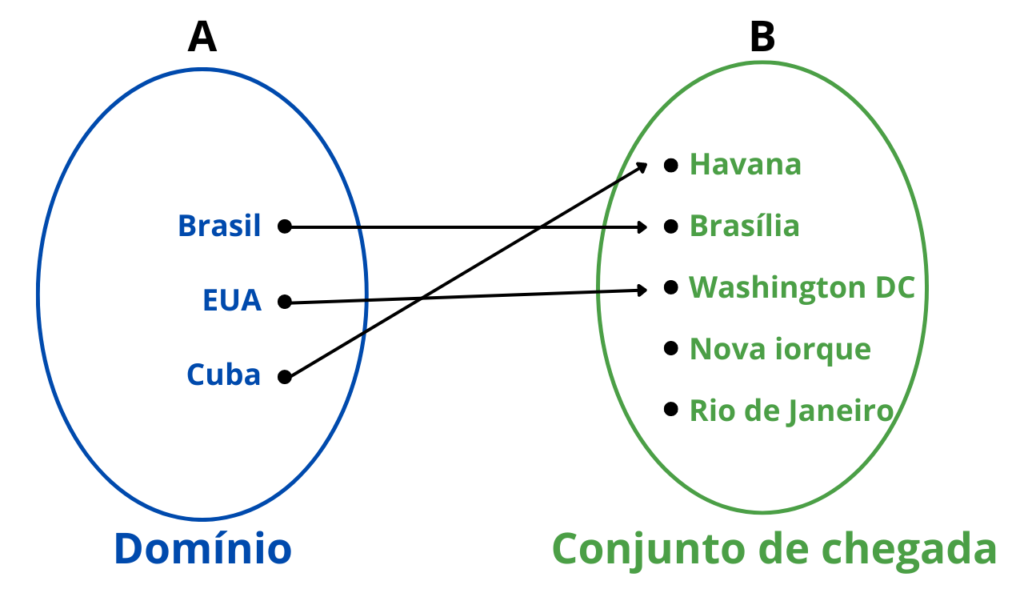
O Pedro e a Paula jogaram o “Jogo das Capitais”. O objetivo do jogo era ligar cada país à sua respetiva capital. Eles tinham a sua frente dois conjuntos de elementos: um conjunto com nomes de países e outro com nomes de cidades.
Posteriormente fizeram as seguintes correspondências:
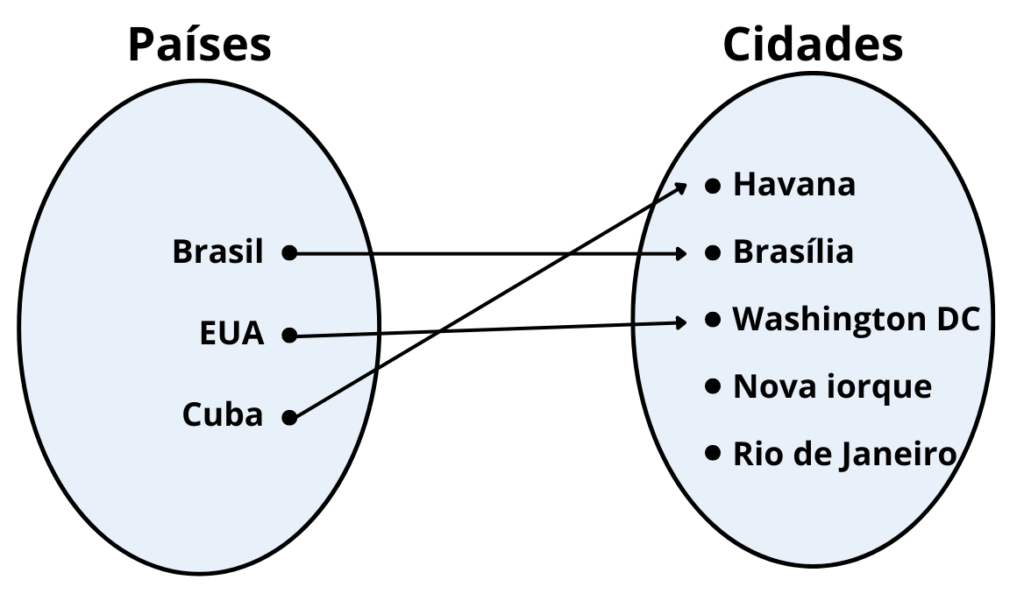
No nosso dia-a-dia, sem nos apercebermos, estamos constantemente a fazer correspondências. Por exemplo:
Essas correspondências têm algo em comum: cada elemento de um conjunto corresponde a um único elemento de outro conjunto.
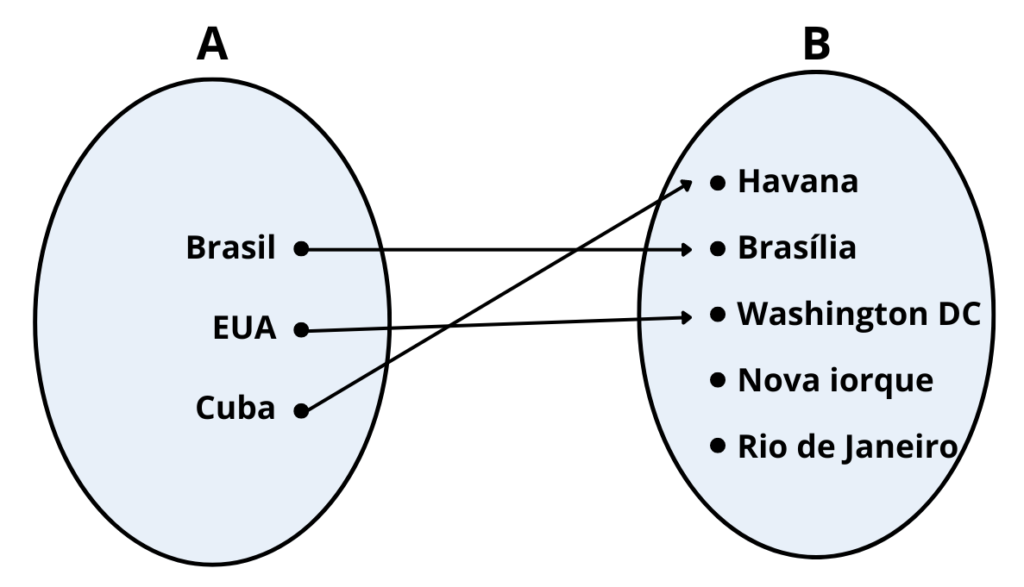
No exemplo anterior, com o Pedro e a Paula, fizemos uma correspondência entre dois conjuntos. Essa correspondência está representada no diagrama de setas seguinte.
Repara que:
Quando uma correspondência verifica estas duas condições, diz-se que é uma função. Ou seja:

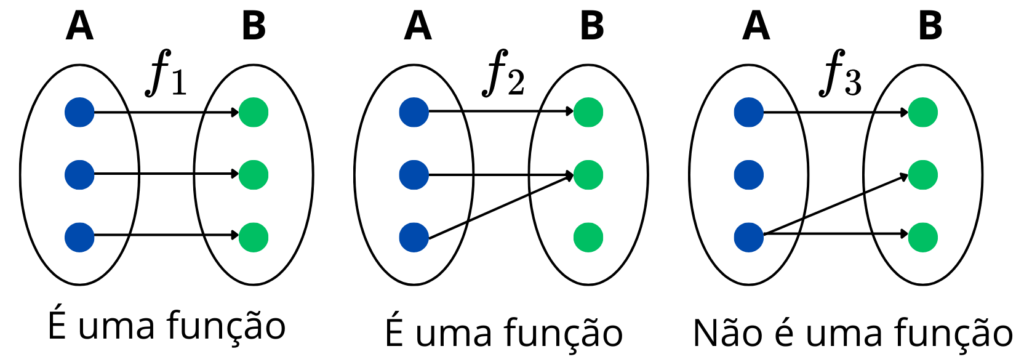
A função f_{3} não representa uma função, pois existe um elemento do domínio sem imagem correspondente e um objeto que tem mais de uma imagem.
Para entender melhor o conceito de funções, é importante introduzir alguns termos específicos: domínio, contradomínio, conjunto de chegada, imagem e objeto. Vamos continuar com o exemplo do “Jogo das Capitais”.
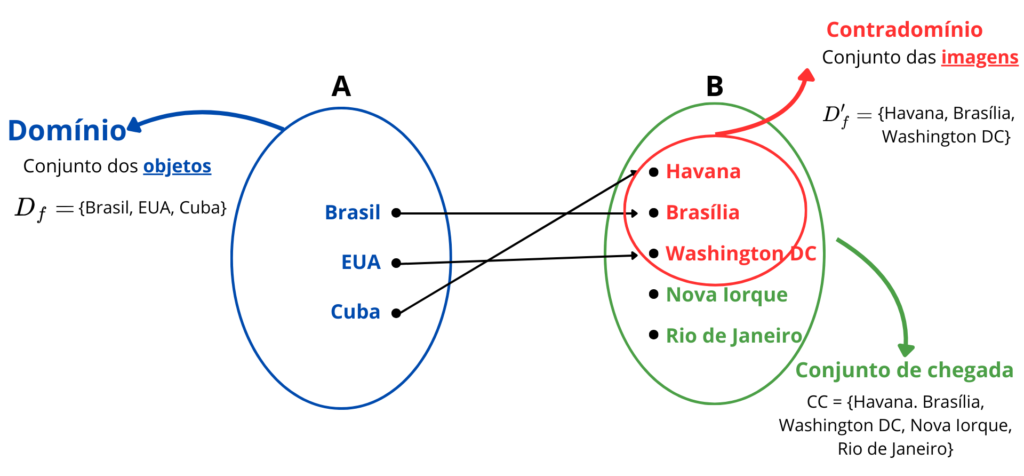
Recapitulando o exemplo anterior, temos o conjunto dos países (domínio) e o conjunto das cidades (conjunto de chegada).
1.Domínio
O domínio de uma função, representado por D_{f}, é o conjunto de todos os elementos de entrada para os quais a função está definida. Cada elemento do domínio é chamado de objeto.
2.Conjunto de Chegada (CC):
O conjunto de chegada é o conjunto onde estão todos os possíveis resultados da função. Cada elemento desse conjunto que corresponde a algum elemento do conjunto A designa-se por imagem.
3.Contradomínio:
Ao conjunto de todas as imagens dá-se o nome de contradomínio e é representado por D’_{f} ou CD_{f}.
Existem várias maneiras de representar uma função. Cada forma de representação pode ser útil dependendo do contexto e do tipo de informação que queremos visualizar ou analisar. As principais formas de representação são:
Vamos utilizar um exemplo para ilustrar cada uma dessas formas de representação.
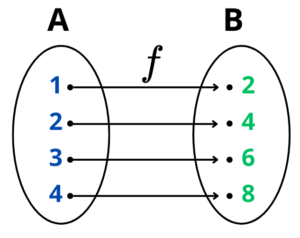
Imaginemos uma função que associa a cada número inteiro do conjunto o seu dobro. Considera os conjuntos A=\left\{ 1,2,3,4 \right\} e B=\left\{ 2,4,6,8 \right\} e a função f:A\to B.
Diagrama de Setas
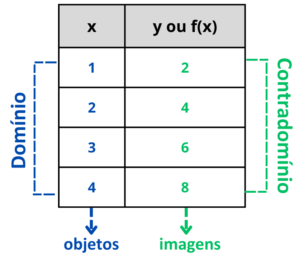
Tabela
As funções também podem ser representadas através de tabelas, onde uma coluna (ou linha) representa os valores do domínio e outra coluna os valores correspondentes no contradomínio (ou imagem).
Expressão Algébrica
Uma expressão algébrica é uma fórmula matemática que descreve a relação entre os elementos do domínio e do contradomínio. No nosso exemplo, a função é definida pela expressão: f(x)=2x
Esta expressão indica que para cada valor de x no domínio, o resultado é o dobro desse valor.
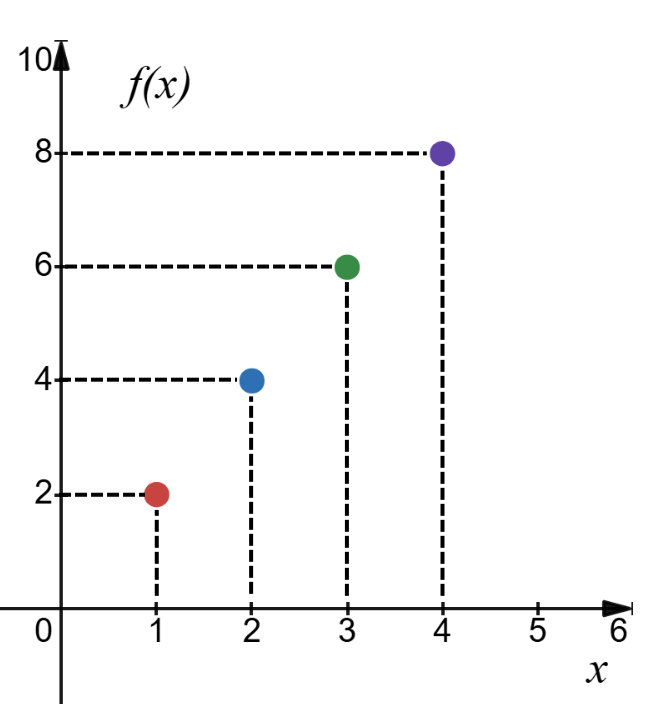
Gráfico Cartesiano
No gráfico cartesiano, a função é representada num plano de duas dimensões. O eixo horizontal (x) representa os valores do domínio, e o eixo vertical (f(x) ou y) representa os valores do contradomínio. Cada par (x,f(x)) é representado como um ponto no gráfico.
Relativamente à função da exemplo anterior, podemos formar os seguintes pares
ordenados: (1,2),(2,4),(3,6),(4,8)
O gráfico cartesiano da função f está representado na figura seguinte.