As equações e expressões algébricas são ferramentas essenciais na matemática, permitindo-nos resolver problemas e compreender relações entre quantidades desconhecidas. Neste artigo, vamos explorar os conceitos básicos de expressões algébricas, a noção de equação, e como resolvê-las de forma simples e prática.
As expressões algébricas são combinações de números, letras (que representam variáveis) e operações matemáticas, como adição, subtração, multiplicação e divisão. São extremamente úteis na matemática, pois nos permitem generalizar situações e resolver problemas.
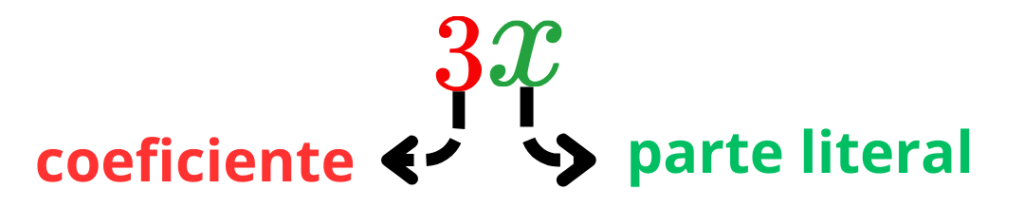
Por exemplo, podemos considerar a soma do triplo de um número com o número dois:

Nesta expressão, o número 3 é chamado de coeficiente, a letra x é a variável, e o número 2 é uma constante.
No exemplo anterior, cada uma das partes da expressão 3x e 2 é chamada de termo. Um termo pode ser um número, uma variável, ou a multiplicação de números e variáveis.
Nos termos que envolvem a multiplicação de um número por uma ou mais letras, ao número chamamos de coeficiente (ou parte literal) e às letras dá-se o nome de parte literal.
Simplificar expressões numéricas
Para usar as expressões numéricas, muitas é preciso simplificá-las. Esse processo consiste em tornar a expressão mais simples, agrupando termos com a mesma parte literal e reduzindo ao máximo o número de operações. Para entender como isso funciona, vamos usar exemplos do dia-a-dia.
Exemplo 1 (Partes literais iguais)
A Maria comprou 4 rebuçados e o Pedro comprou 6 rebuçados. Cada rebuçado custa y euros. Quanto gastaram os dois amigos juntos?

Resolução:
Podemos representar o custo dos rebuçados da Maria como 4y euros e o custo dos rebuçados do Pedro como 6y euros.
Então, a expressão que representa o custo total é: 4y+6y
Como as expressões 4y e 6y têm a mesma parte literal (y), são chamadas de termos semelhantes.
Para simplificar a expressão, somamos apenas os coeficientes dos termos semelhantes, mantendo a parte literal: 4y+6y=10y
Dessa forma, os dois amigos gastaram juntos 10y euros.

Exemplo 2 (Partes literais diferentes)
Considera a seguinte moldura triangular com os comprimentos dos lados apresentados.
Resolução:
Para calcular o perímetro do triângulo, somamos os comprimentos dos três lados:
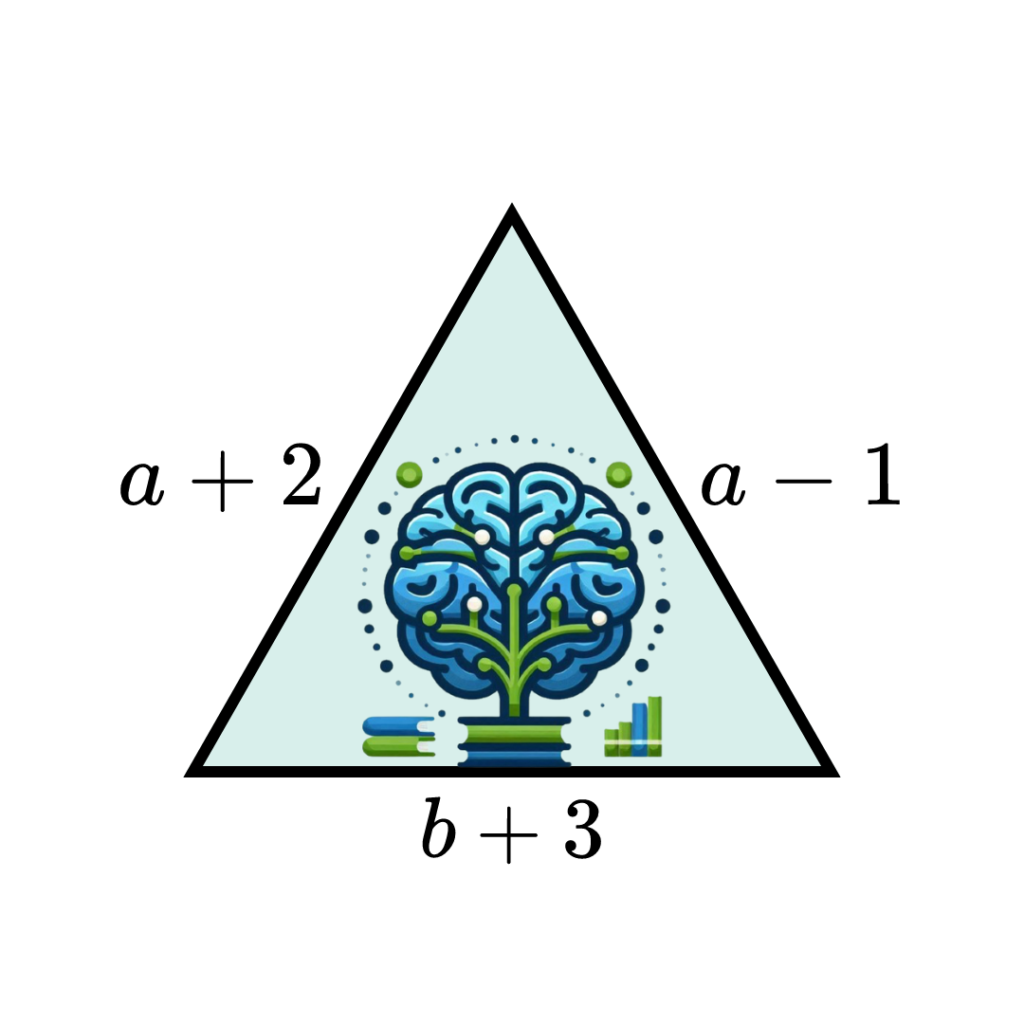
Perímetro=(a+2)+(b+3)+(a-1)
Agora, vamos simplificar esta expressão. Primeiro, agrupamos os termos semelhantes e somamos as partes numéricas:
=a+a+b+2+3-1
Depois de organizar e simplificar, obtemos:
=2a+b+4
Já não é possível simplificar mais, pois as expressões 2a, b e 4 têm partes literais diferentes.
Uma equação é uma igualdade entre duas expressões numéricas. São sempre divididas por um sinal de igual (=).
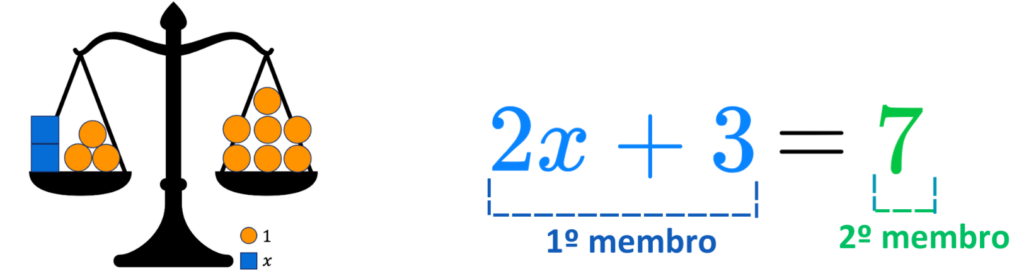
As equações são utilizadas para encontrar o valor desconhecido de uma variável que torna a equação verdadeira. Para representar este valor desconhecido, usamos uma letra. Por exemplo, na equação 2x+3=7, o nosso objetivo é descobrir qual o valor de x que faz com que a equação seja verdadeira.
Os termos que contêm a variável desconhecida são chamados de termos com incógnita, enquanto os termos que não contêm a incógnita são chamados de termos independentes.
Exemplo 3
Na equação 2x+3=-4x+7:

Resolver uma equação significa encontrar o valor da incógnita que torna a equação verdadeira. Para isso, deves seguir alguns passos simples:
1.Organizar os Termos com Incógnita e Termos Independentes:
Começa por reorganizar a equação, ao “passar” todos os termos com incógnita para um lado do sinal de igual e todos os termos independentes para o outro lado. Para fazer isso, ao mudar um termo de um lado para o outro, deves alterar o sinal do termo que estás a “mover”.
Exemplo: Na equação 2x+3=7, queremos passar o termo independente (3) para o outro lado: 2x=7-3
2.Simplificar as Expressões:
Agora, simplifica as expressões em ambos os lados da equação, realizando as operações necessárias. No nosso exemplo, subtraímos 7 por 3: 2x=4
3.Isolar a Incógnita:
Para encontrar o valor de x, precisas de isolar a incógnita. Para isso, divide ambos os lados da equação pelo coeficiente do termo com incógnita (neste caso, 2): x=\frac{4}{2}
O resultado é: x=2
4.Escrever o Conjunto-Solução:
Após isolar a incógnita, o valor obtido é a solução da equação. Escreve a solução de forma clara. Neste exemplo, a solução é x=2. O conjunto-solução pode ser escrito como: C.S=\left\{ 2 \right\}
Existem diferentes abordagens para compreender e resolver uma equação. Estes passos fornecem uma metodologia clara e prática para a sua resolução. Nos próximos artigos, exploraremos outras formas de entender os processos envolvidos na resolução de equações.