Quando pensamos em figuras geométricas, muitas vezes imaginamos formas planas como quadrados, triângulos e círculos. No entanto, o mundo ao nosso redor está repleto de formas tridimensionais, ou figuras no espaço, que ocupam volume e têm profundidade. Essas formas podem ser encontradas na arquitetura, na natureza e em objetos do quotidiano.
Neste capítulo, vamos mergulhar no fascinante mundo das figuras no espaço, começando pelos poliedros.
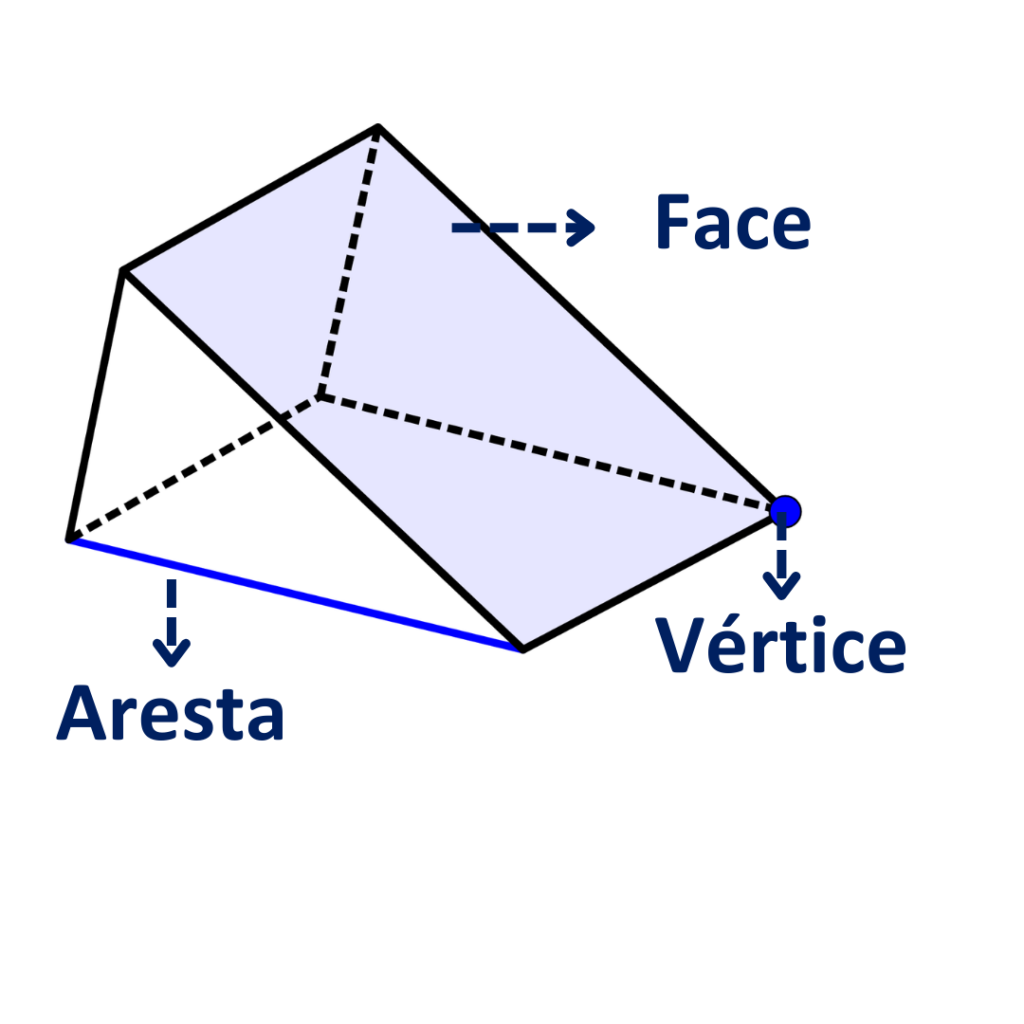
Um poliedro é uma figura geométrica tridimensional formada por várias superfícies planas, chamadas faces. Essas faces são polígonos (como triângulos, quadrados ou pentágonos), e cada par de faces interseta-se ao longo de uma linha reta chamada aresta. Os pontos onde as arestas se intersetam são chamados de vértices.
Alguns exemplos comuns de poliedros incluem:
Cubo
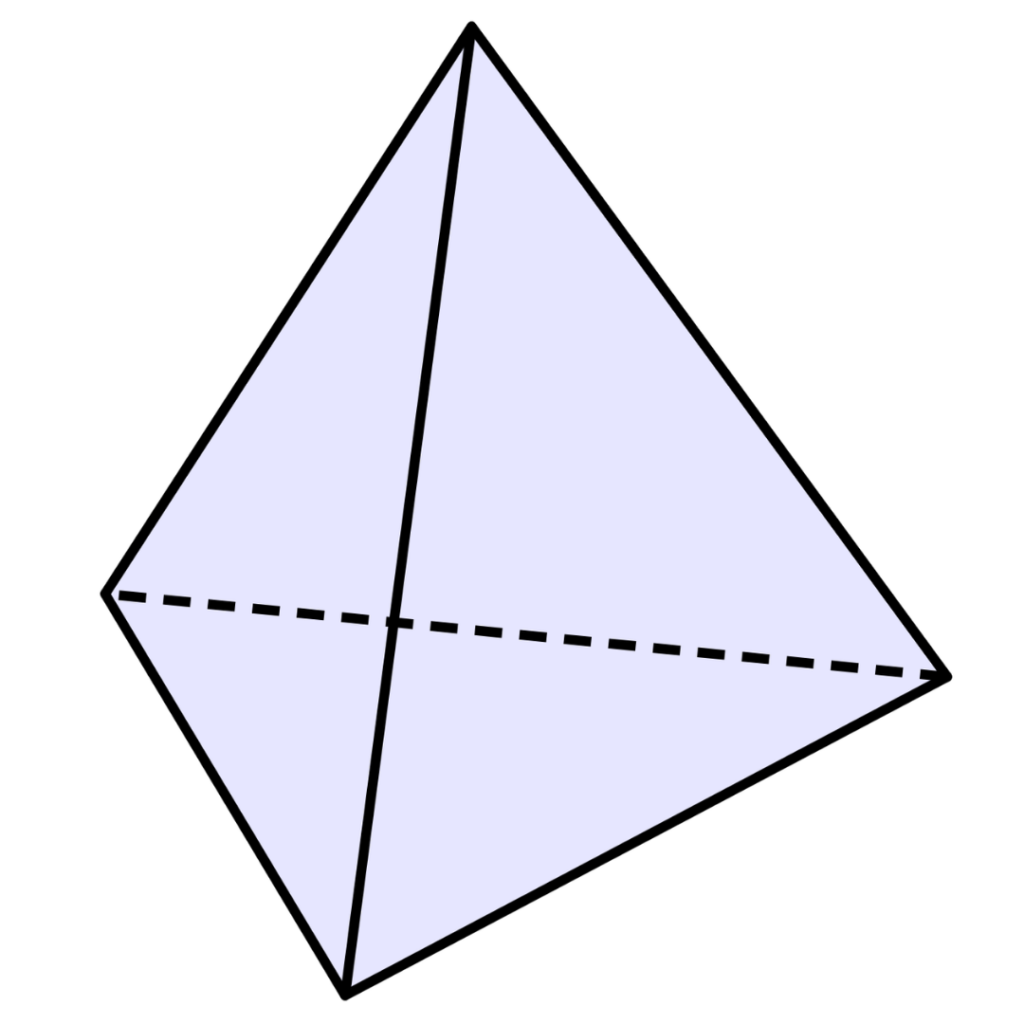
Tetraedro
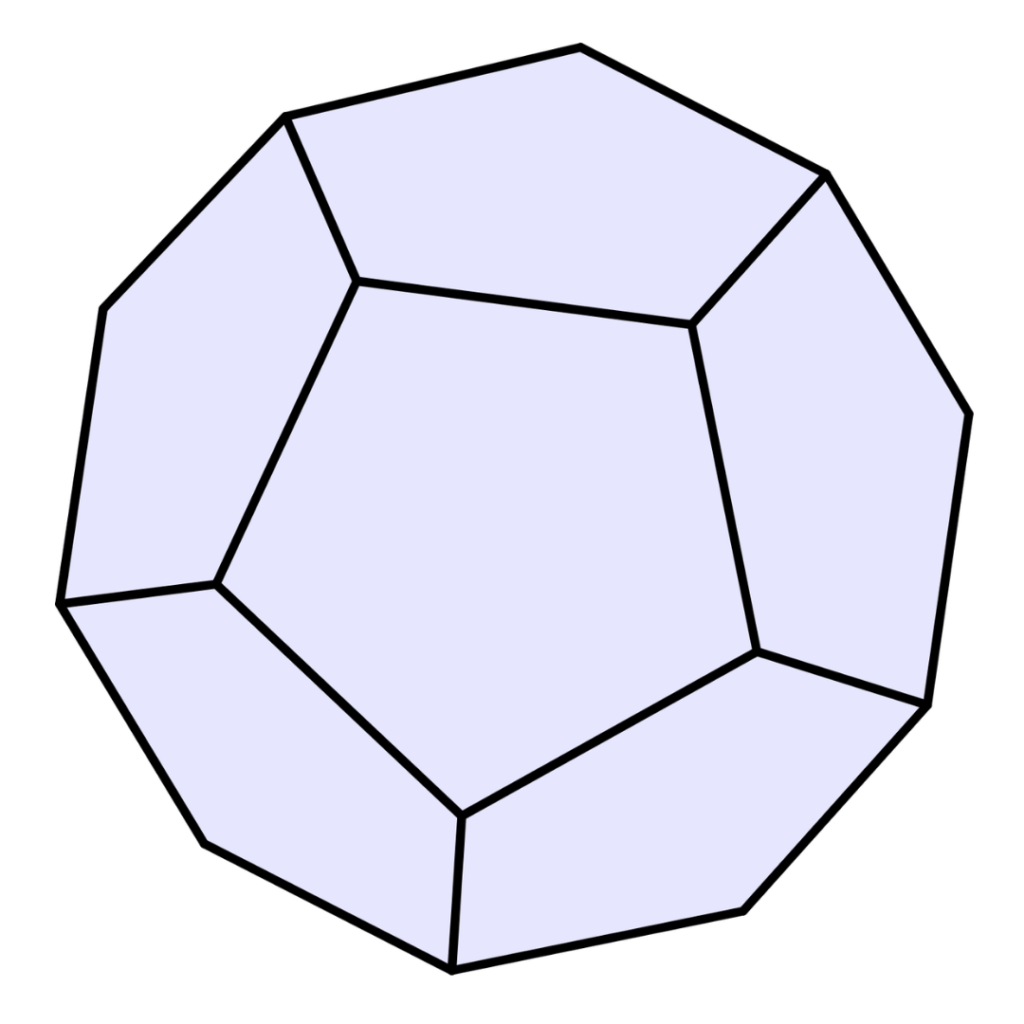
Dodecaedro
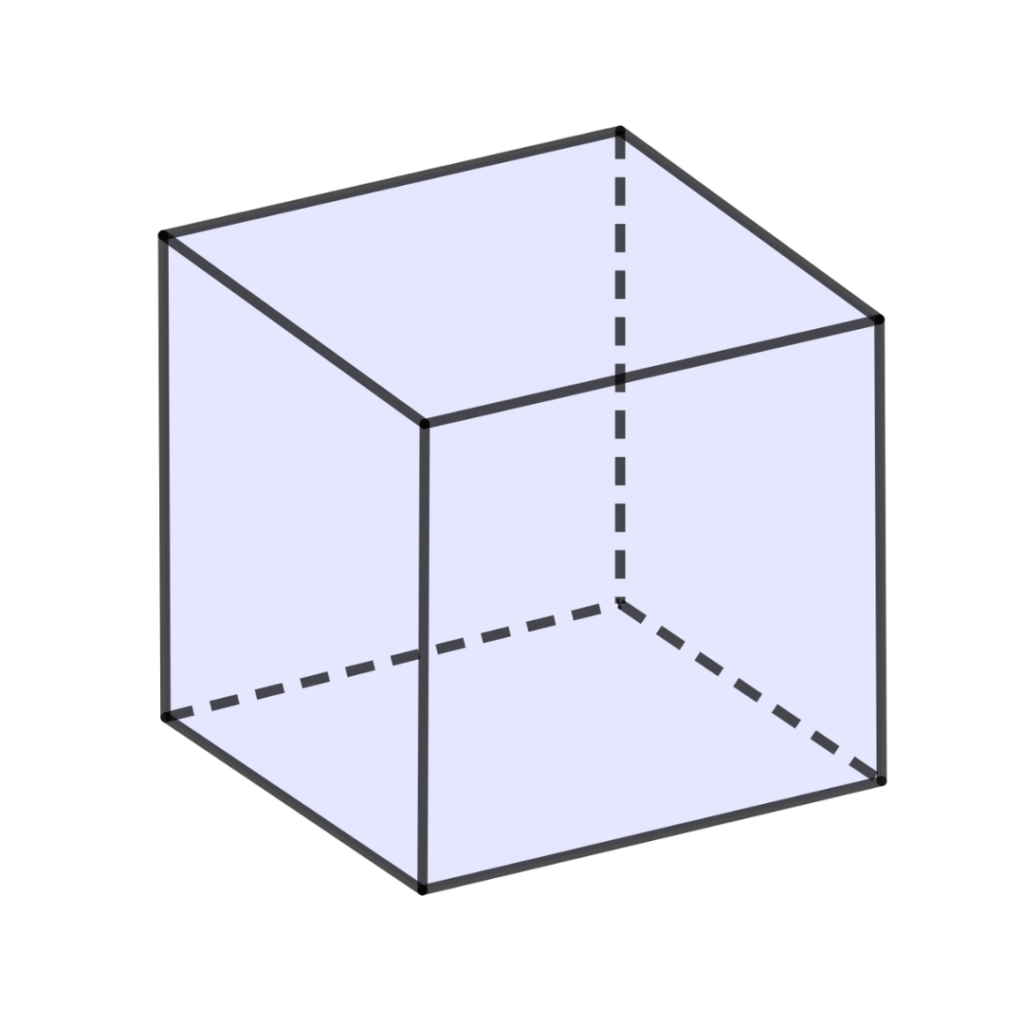
6 faces quadradas
4 faces triangulares
12 faces pentagonais
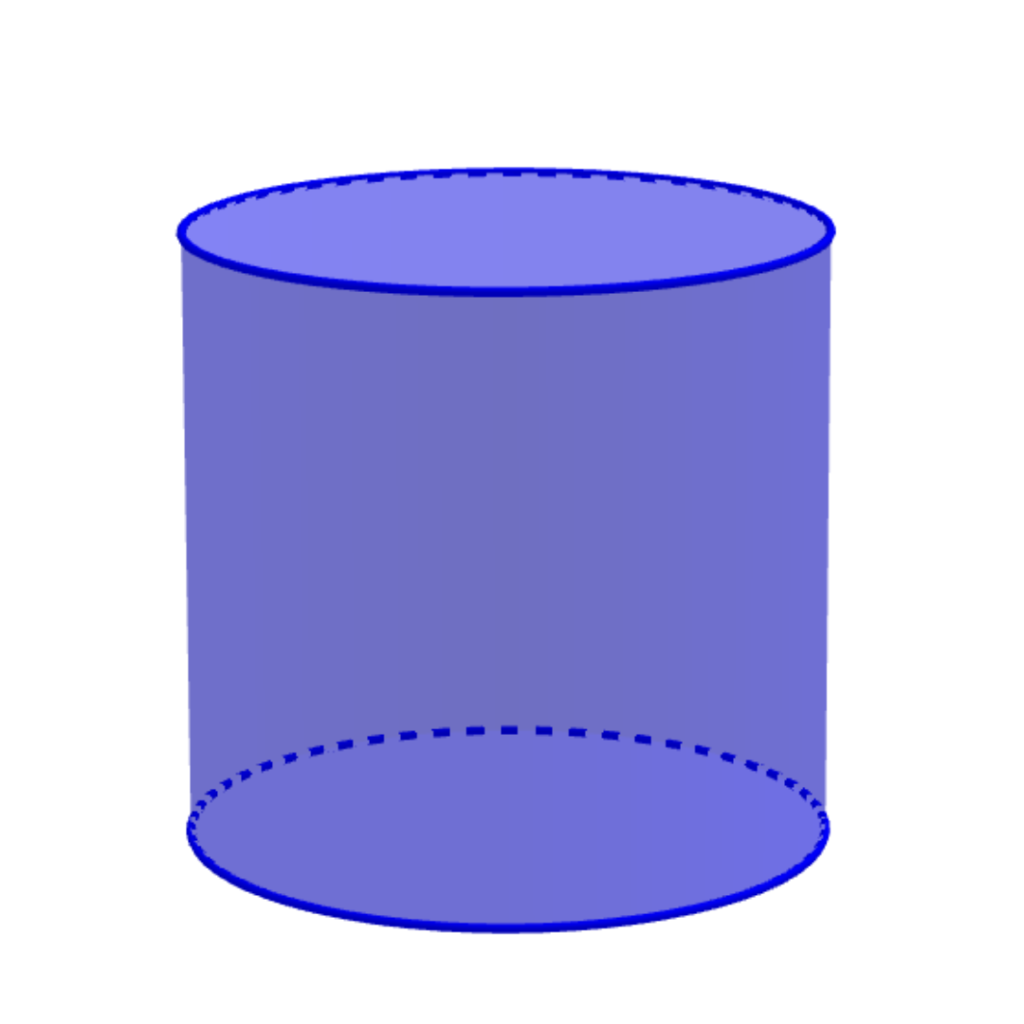
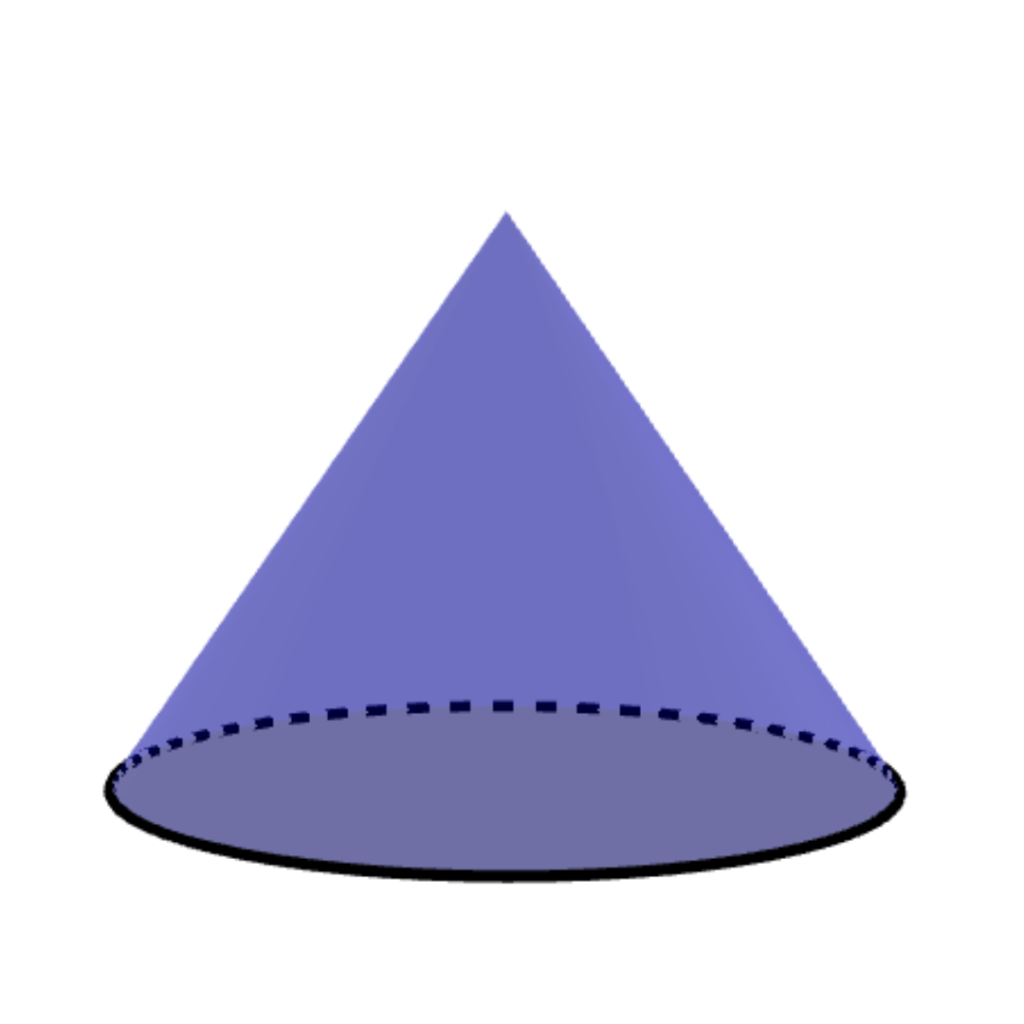
Nem todas as figuras tridimensionais são poliedros. Figuras que possuem superfícies curvas, como esferas, cilindros e cones, são consideradas não poliedros.
Esfera
Cone
Cilindro

À semelhança dos polígonos, os poliedros podem ser classificados como convexos ou côncavos.
Convexos
Côncavos
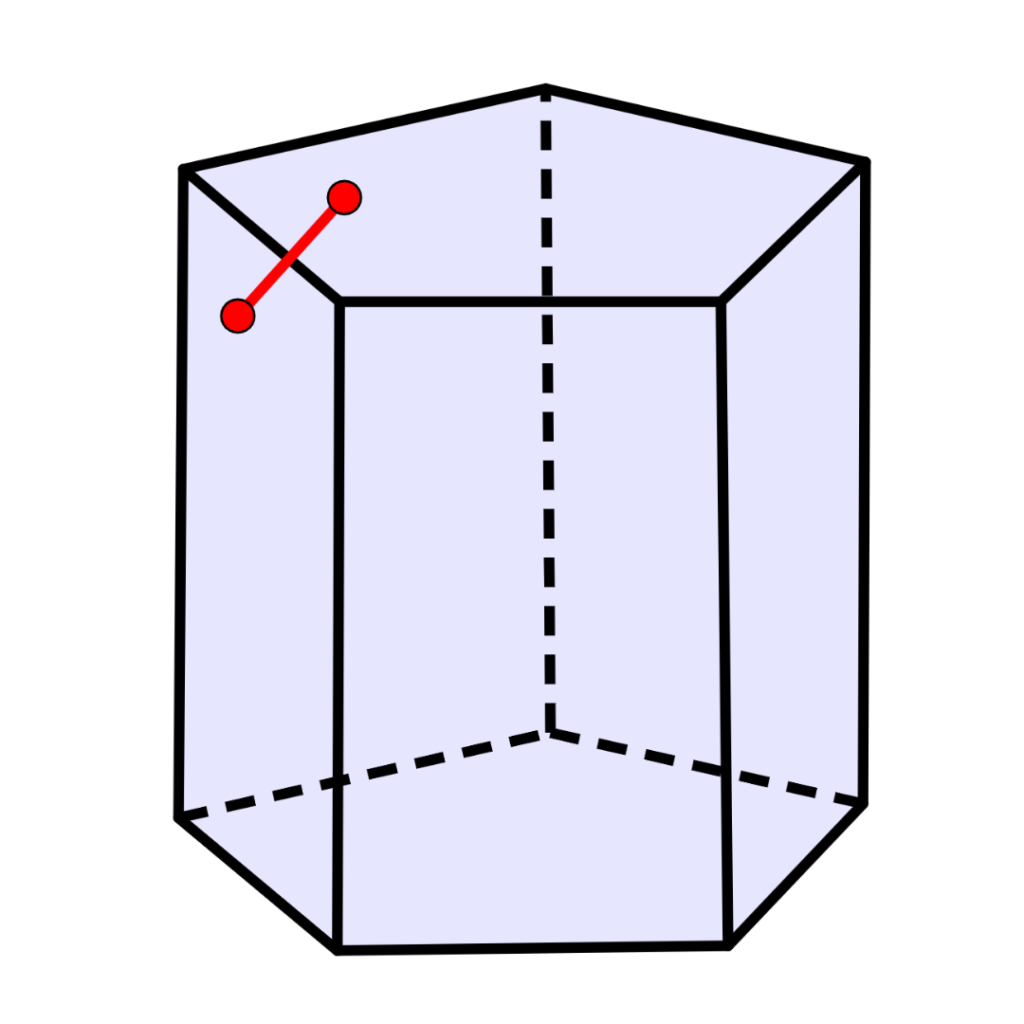
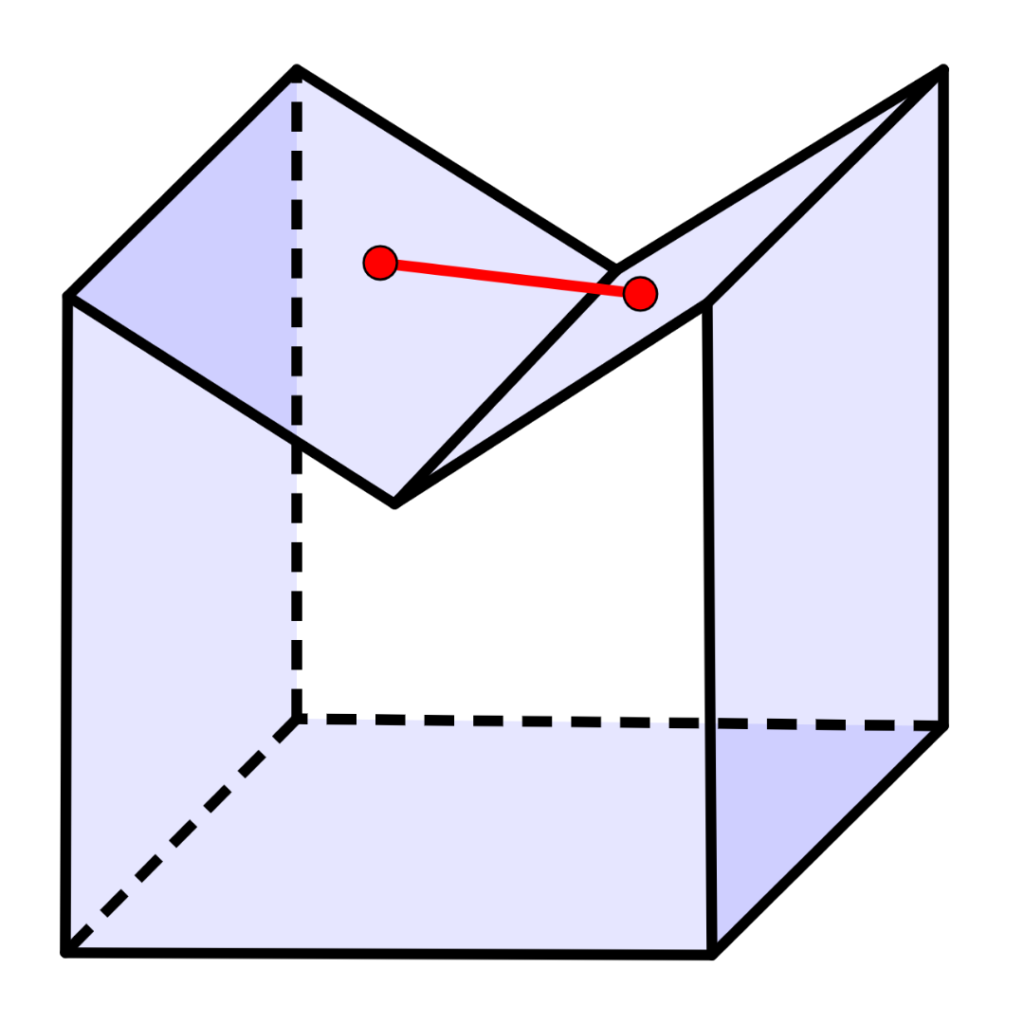
São aqueles em que qualquer segmento de reta que ligue dois pontos no interior do poliedro está completamente dentro do poliedro.
Pode-se desenhar um segmento de reta entre dois pontos dentro do poliedro que passa por fora do poliedro. Por outras palavras, possuem alguma parte “afundada” para dentro.
– Classificação dos poliedros
Os poliedros podem ser classificados dependendo do número de faces, do formato das faces e da regularidade da figura:
Existem exatamente cinco poliedros regulares, conhecidos como sólidos platónicos. Estes são:
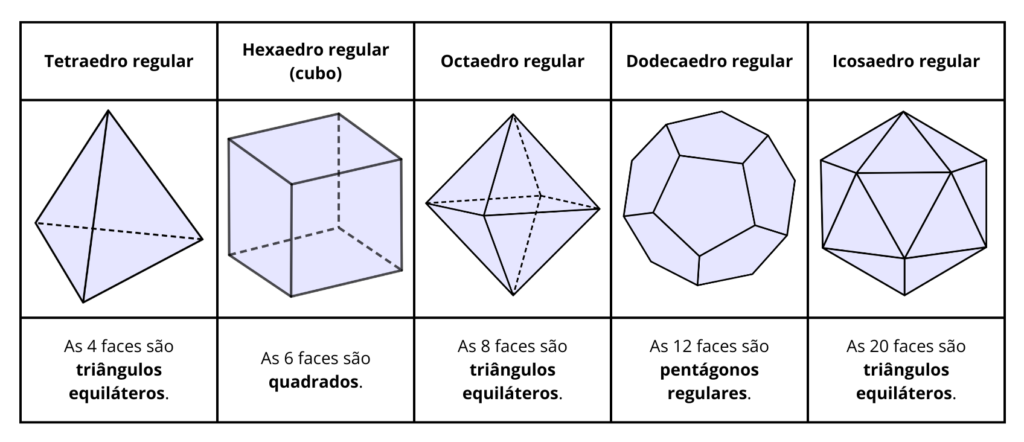
Nos próximos artigos abordaremos melhor estes cinco sólidos.
A Fórmula de Euler é uma relação importante em geometria que conecta o número de vértices (V), arestas (A) e faces (F) de um poliedro convexo. A fórmula é expressa como:
$$V−A+F=2$$
Em que:
Exemplo
Consideremos o cubo. Este tem:
Aplicando a fórmula de Euler tem-se:
$$8-12+6 = 2$$

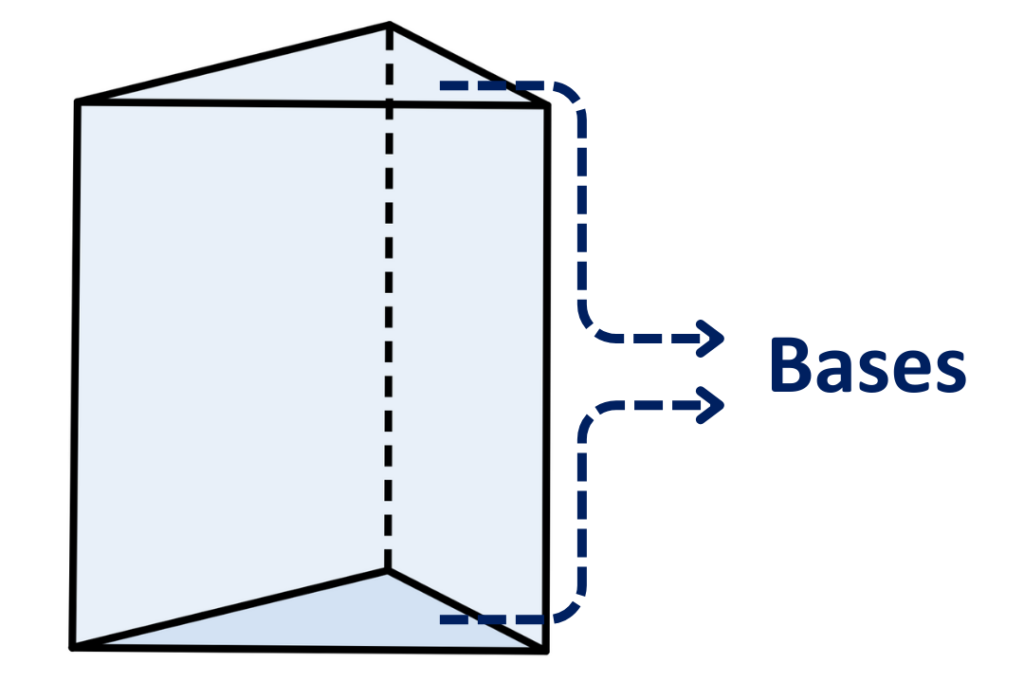
Um prisma é um tipo especial de poliedro caracterizado por duas faces paralelas e iguais chamadas bases. As outras faces do prisma, chamadas de faces laterais, são paralelogramos (quadriláteros com lados opostos paralelos).
Um prisma reto é aquele cujas faces laterais são retângulos. Caso contrário, denomina-se por prisma oblíquo.
Um prisma regular é um prisma reto cujas bases são polígonos regulares. Alguns exemplos são:
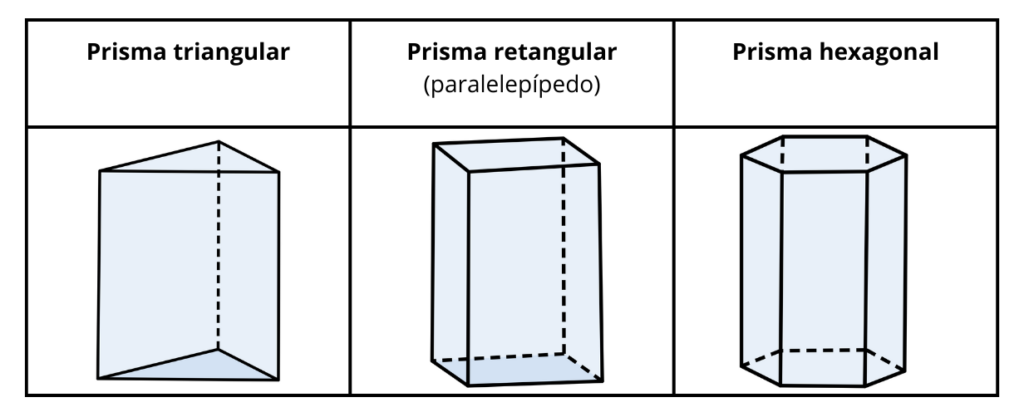
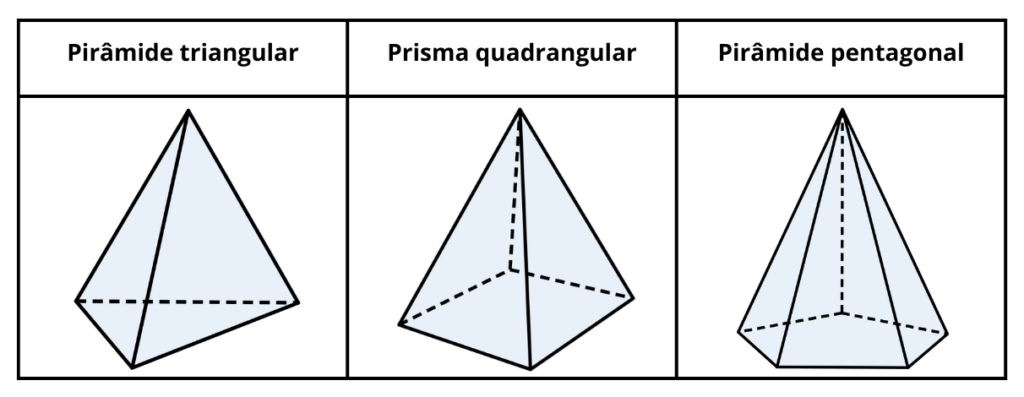
Uma pirâmide é um poliedro que tem uma base (que pode ser qualquer polígono) e um ponto chamado vértice, que não está no mesmo plano da base. As faces laterais de uma pirâmide são sempre triângulos.
As pirâmides são classificadas de acordo com a forma da sua base, como por exemplo: