As figuras planas são formas bidimensionais fundamentais na geometria, representando áreas delimitadas por lados e vértices em um plano. Neste capítulo, exploraremos as áreas de figuras comuns como triângulos, quadrados, retângulos, paralelogramos, trapézios e papagaios, apresentando as fórmulas essenciais para calcular a área de cada uma. Entender essas fórmulas é crucial para aplicações práticas e teóricas, permitindo a análise precisa do espaço que essas figuras ocupam.
Os polígonos são figuras geométricas planas delimitadas por segmentos de reta consecutivos que formam um caminho fechado.
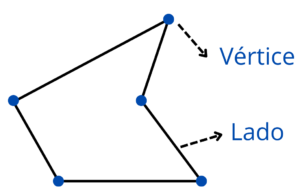
Cada segmento de reta é chamado de lado do polígono e o ponto onde dois lados se encontram é chamado de vértice.
Os polígonos podem ter vários números de lados e recebem nomes específicos de acordo com esse número, como triângulo (3 lados), quadrilátero (4 lados), pentágono (5 lados), entre outros.

Os polígonos podem ser convexos ou côncavos:
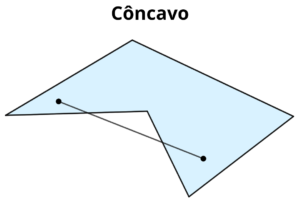
Um polígono é côncavo se pelo menos um segmento de reta que une dois pontos do polígono estiver fora do polígono. Há pelo um ângulo interno com mais de 180º
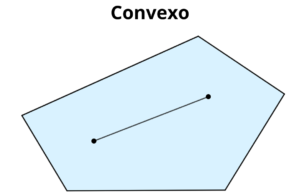
Um polígono é convexo quando qualquer segmento de reta que une dois pontos do polígono está inteiramente contido no polígono.
Adicionalmente, todos os seus ângulos internos são menores que 180º.
A diagonal de um polígono é um segmento de reta que conecta dois vértices não consecutivos.
Para calcular o número de diagonais de um polígono com lados (ou vértices), usamos a seguinte fórmula: D=\frac{n(n-3)}{2}
Exemplo
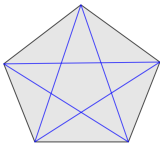
Para o exemplo do pentágono ao lado (n=5), o número de diagonais é: D=\frac{5(5-3)}{2}=5
Como se pode comprovar com a figura.
Os ângulos são uma das principais componentes da geometria e têm aplicações em diversas áreas da matemática e da ciência. Eles são formados pela interseção de duas linhas ou segmentos de reta em um ponto comum, chamado vértice
Um ângulo é a medida da abertura entre duas semirretas que partem de um ponto comum, denominado vértice do ângulo. A unidade de medida dos ângulos é o grau (º).
Os ângulos podem ser classificados de acordo com sua amplitude em diferentes categorias:
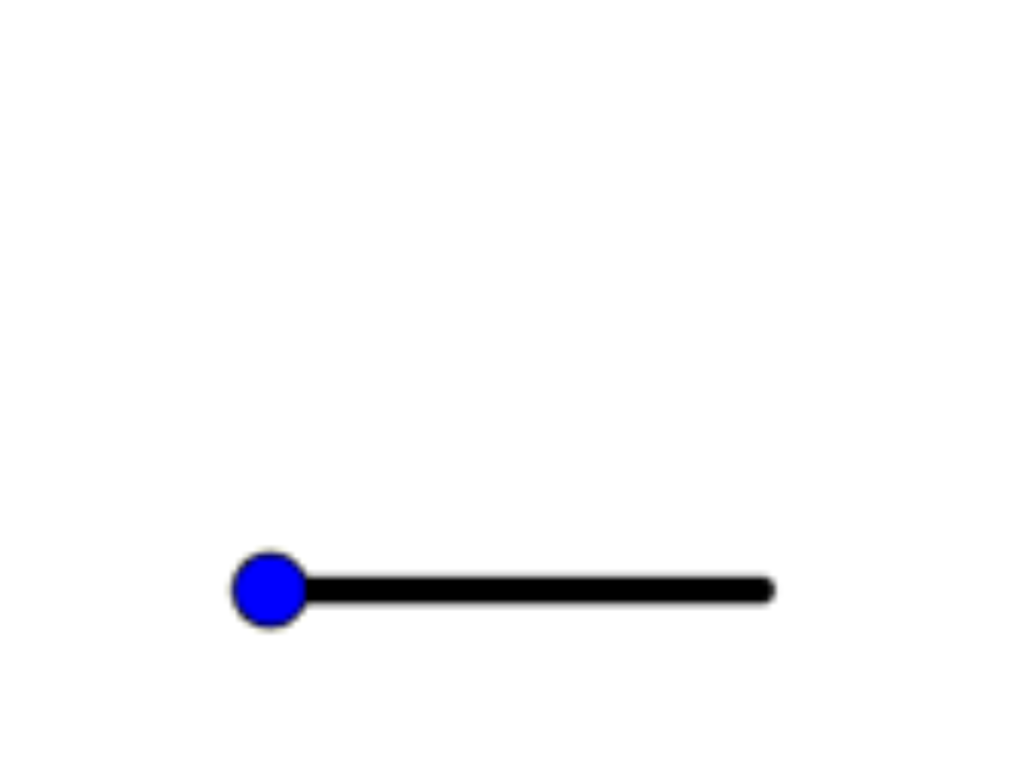
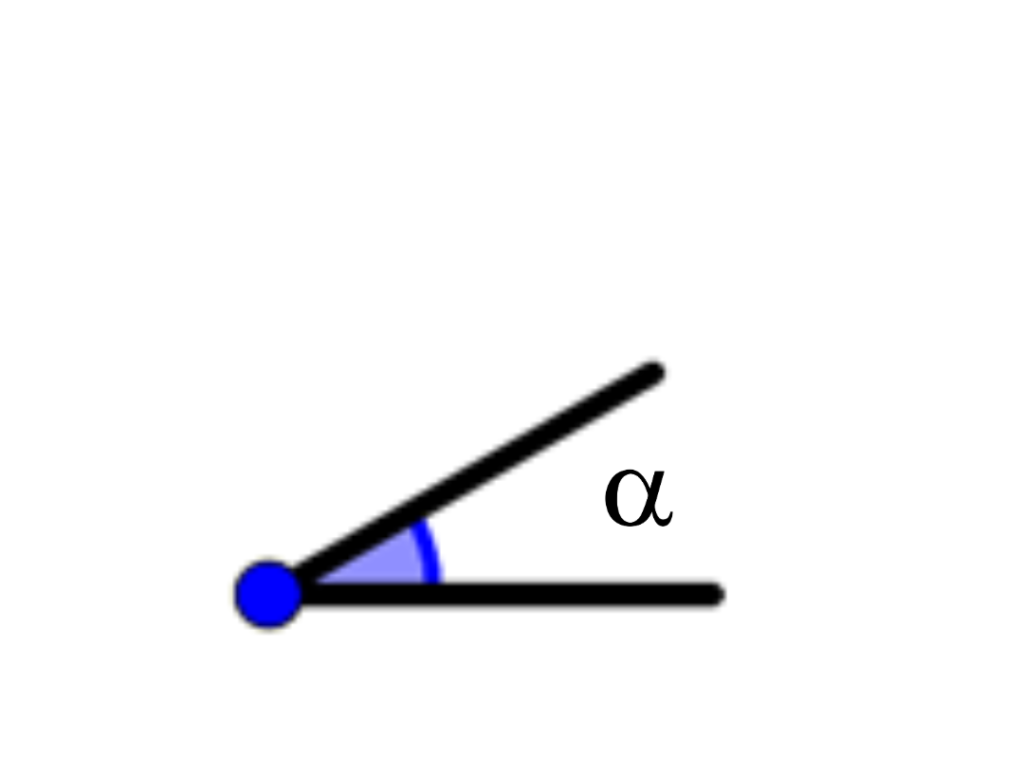
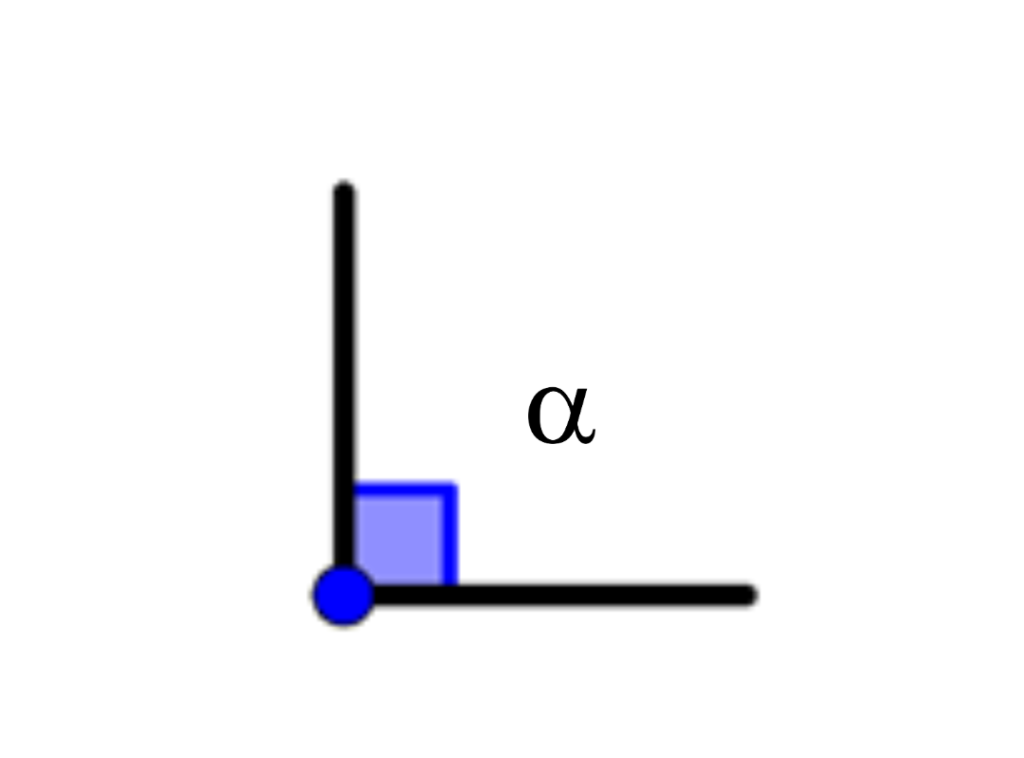
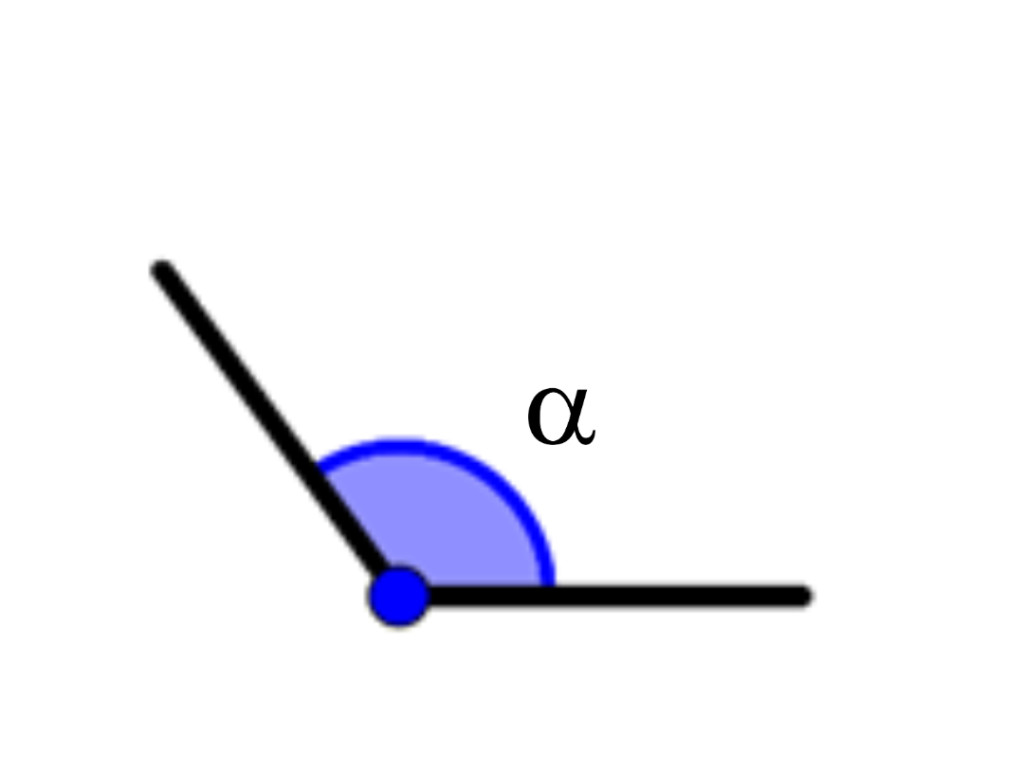
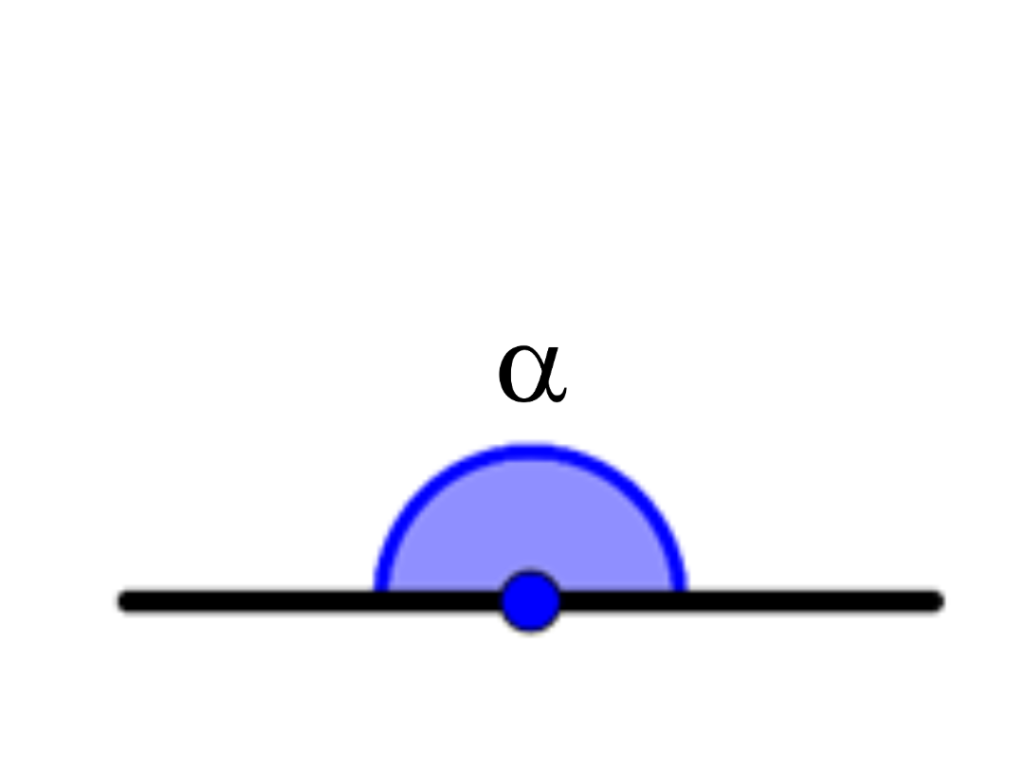
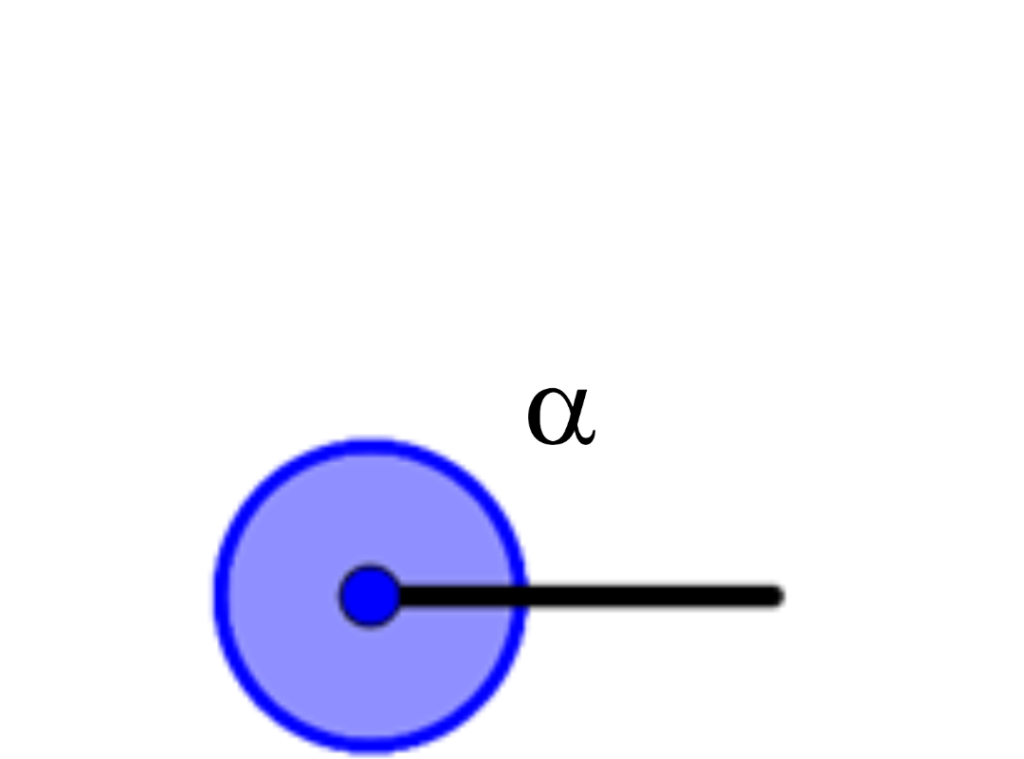
\alpha=0^{º}
0^{º}\lt \alpha\lt 90^{º}
\alpha=90^{º}
90^{º}\lt \alpha\lt 180^{º}
\alpha=180^{º}
\alpha=360^{º}
Ângulo nulo
Ângulo agudo
Ângulo reto
Ângulo obtuso
Ângulo raso
Ângulo giro
Além de serem classificados pela sua amplitude, os ângulos também podem ser relacionados uns com os outros de diversas maneiras. Aqui estão algumas das relações mais comuns:
Dois ângulos são adjacentes quando compartilham um vértice e um lado comum, mas não têm pontos internos em comum.
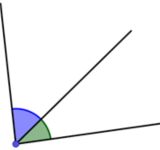
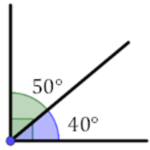
Dois ângulos são complementares quando a soma das suas medidas é igual a 90 graus. Eles podem ou não ser adjacentes.
Adjacentes
Não adjacentes
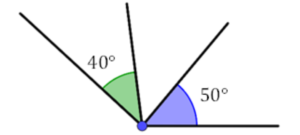
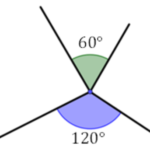
Dois ângulos são suplementares quando a soma das suas medidas é igual a 180 graus. Eles também podem ou não ser adjacentes.
Adjacentes
Não adjacentes

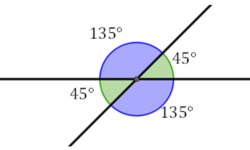
Dois ângulos são verticalmente opostos quando são formados pela interseção de duas retas. Eles mesmos ângulos têm a mesma amplitude.
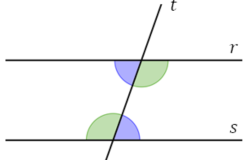
Ângulos alternos internos são formados quando uma transversal (t) cruza duas linhas paralelas (r e s) .
Eles estão localizados em lados opostos da transversal e dentro das duas linhas paralelas. Esses ângulos têm também sempre a mesma amplitude.
Já aprendeste que os polígonos são figuras geométricas formadas por uma sequência de segmentos de reta conectados, criando um caminho fechado. Eles desempenham um papel fundamental na geometria e aparecem em inúmeras aplicações, desde a arte e design até a arquitetura e engenharia. Compreender os ângulos internos e externos desses polígonos é essencial para explorar suas propriedades e resolver problemas geométricos.
Definição
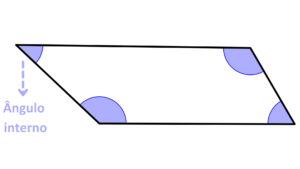
Um ângulo interno de um polígono é o ângulo formado entre dois lados consecutivos do polígono que se encontram em um vértice. Em outras palavras, é o ângulo dentro do polígono entre duas arestas adjacentes.
Soma dos Ângulos Internos
A soma dos ângulos internos de um polígono depende do número de lados do polígono e pode ser calculada usando a fórmula:
Soma dos ângulos internos=(n-2)\times 180^{º}
onde n é o número de lados do polígono.
Exemplo
Dividindo o Polígono em Triângulos
Uma maneira alternativa de entender e calcular a soma dos ângulos internos de um polígono convexo é dividindo-o em triângulos não sobrepostos. Para isso, basta traçar diagonais a partir de um vértice de referência que o liguem a todos os outros vértices.
Quadrilátero
Pentágono
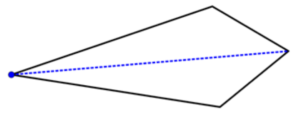
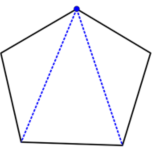
Esta abordagem é baseada no fato de que a soma dos ângulos internos de um triângulo é sempre 180 graus. Vamos aplicar esse método ao hexágono do exemplo anterior.
Exemplo
\textbf{4}\times180^{º}=720^{º}
\textbf{(6-2)}\times180^{º}=720^{º} (como se verifica na fórmula)
Definição
Um ângulo externo de um polígono é um ângulo suplementar e adjacente ao correspondente ângulo interno do polígono. Por outras palavras, é o ângulo formado fora do polígono, entre um lado e a continuação do lado adjacente.
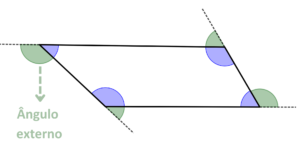
Soma dos Ângulos Externos
A soma dos ângulos externos de qualquer polígono é sempre 360 graus.
Os triângulos são uma das formas geométricas mais fundamentais e estudadas na Matemática. Eles consistem em três lados e três ângulos, sendo os elementos básicos para entender formas mais complexas. Nesta secção vamos fazer uma revisão de algumas propriedades essenciais dos triângulos, incluindo a desigualdade triangular, a soma dos ângulos internos e externos, e a classificação dos triângulos quanto aos lados e ângulos.
Desigualdade Triangular
A desigualdade triangular é uma propriedade fundamental dos triângulos. Ela afirma que, num triângulo, o comprimento de um lado qualquer é menor que a soma dos comprimentos dos outros dois.
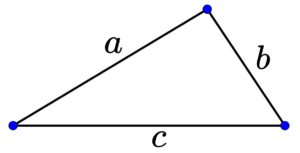
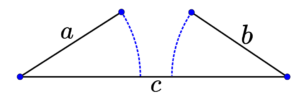
Essa propriedade garante que os três segmentos de reta possam formar um triângulo. Se a desigualdade não for satisfeita, então não é possível formar um triângulo com esses lados.
Soma dos ângulos internos e externos
A soma dos ângulos internos é sempre igual a 180 graus.
A soma dos ângulos internos é sempre igual a 360 graus.
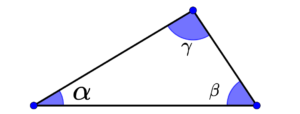
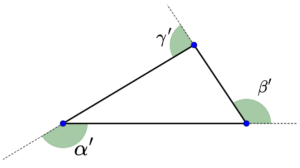
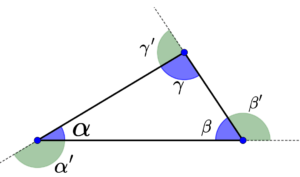
Uma propriedade importante é que a medida de um ângulo externo é igual à soma dos dois ângulos internos não adjacentes.
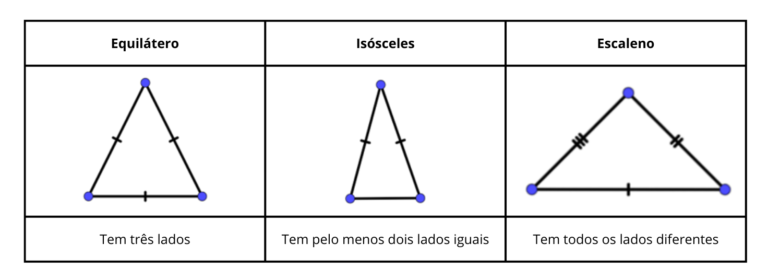
Os triângulos podem ser classificados de duas maneiras: pelo comprimento de seus lados e pela medida de seus ângulos.
– Quanto aos lados
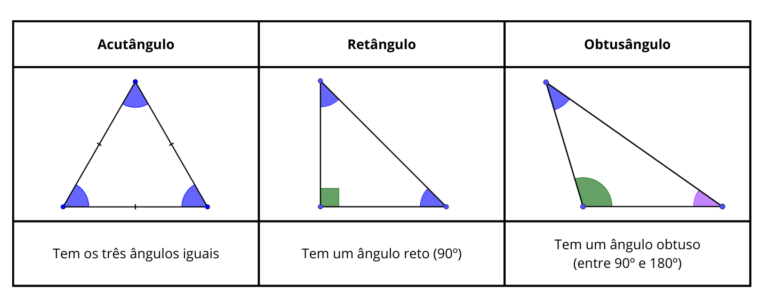
– Quanto aos ângulos
Dois triângulos são geometricamente iguais (ou congruentes) quando têm exatamente a mesma forma e o mesmo tamanho. Isso significa que todos os lados correspondentes são iguais em comprimento e todos os ângulos correspondentes são iguais em medida.
No entanto, não é necessário demonstrar que os três lados e ângulos correspondentes são iguais. Para isso, podemos recorrer aos critérios de igualdade de triângulos.
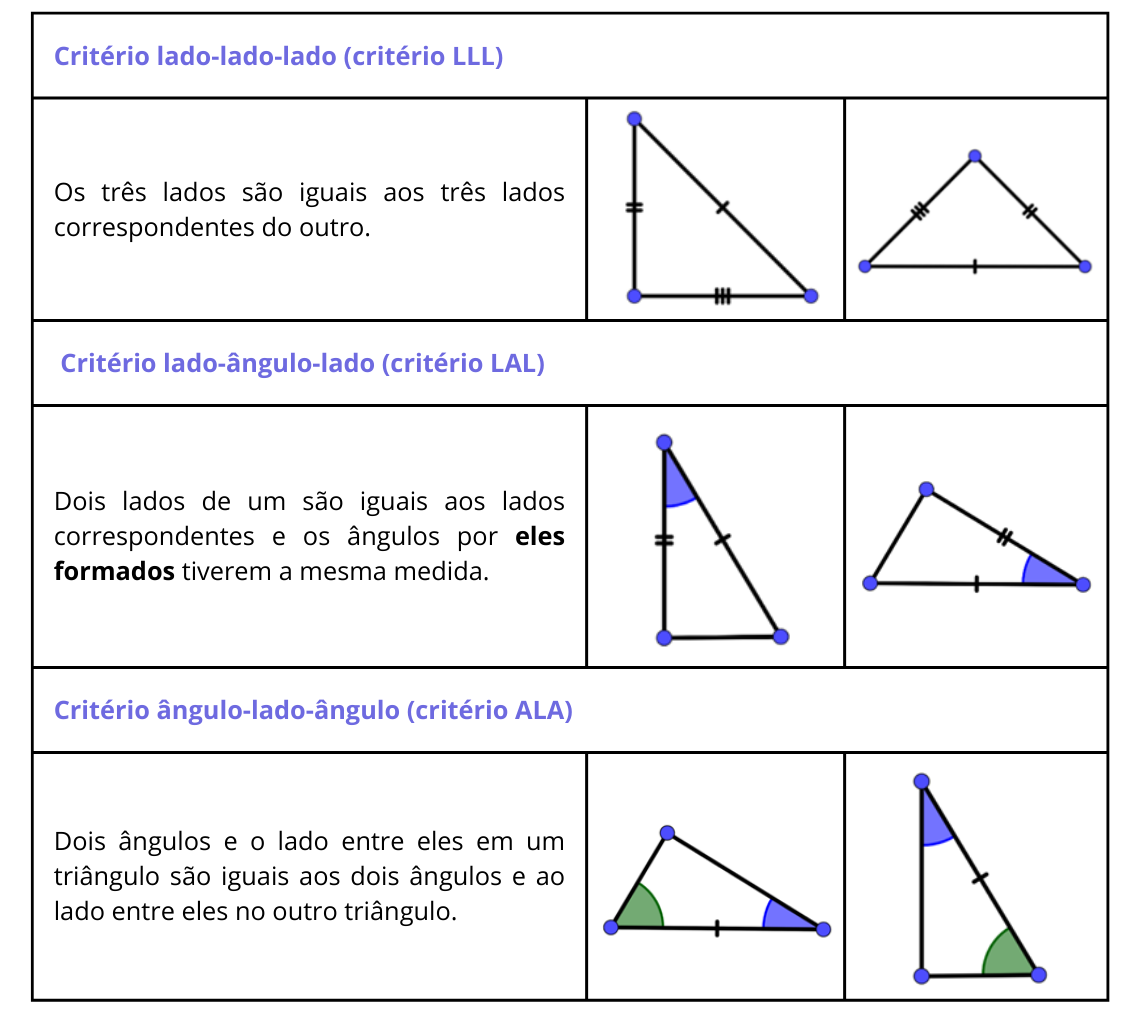
Dois triângulos são iguais se:
Quadriláteros são polígonos com quatro lados e quatro vértices. Uma característica importante dos quadriláteros é que eles possuem exatamente duas diagonais, que são segmentos de linha que conectam vértices opostos. Dependendo das propriedades dos seus lados e ângulos, os quadriláteros podem ser classificados em várias categorias, incluindo trapézios, papagaios, paralelogramos, e seus subtipos, como retângulos, losangos e quadrados.
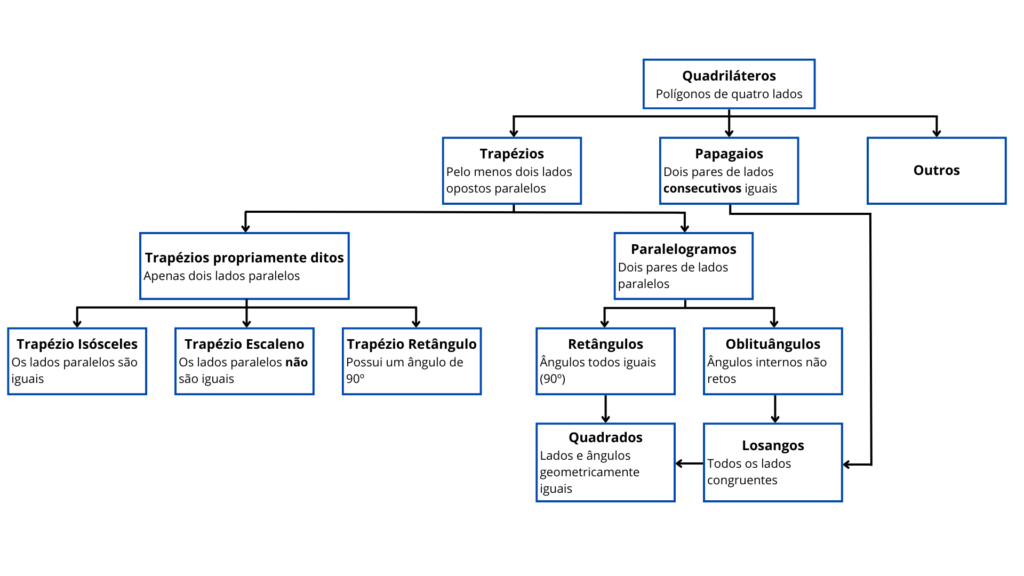
Classificação dos Quadriláteros
A. Trapézio
Um trapézio é um quadrilátero que possui pelo menos um par de lados opostos paralelos. Os lados paralelos são chamados de bases, enquanto os outros dois lados são as laterais. Os trapézios podem ser subdivididos em:
Tem ambos os pares de lados opostos paralelos. Nesse caso, o trapézio é, na verdade, um paralelogramo, que inclui retângulos, losangos e quadrados.
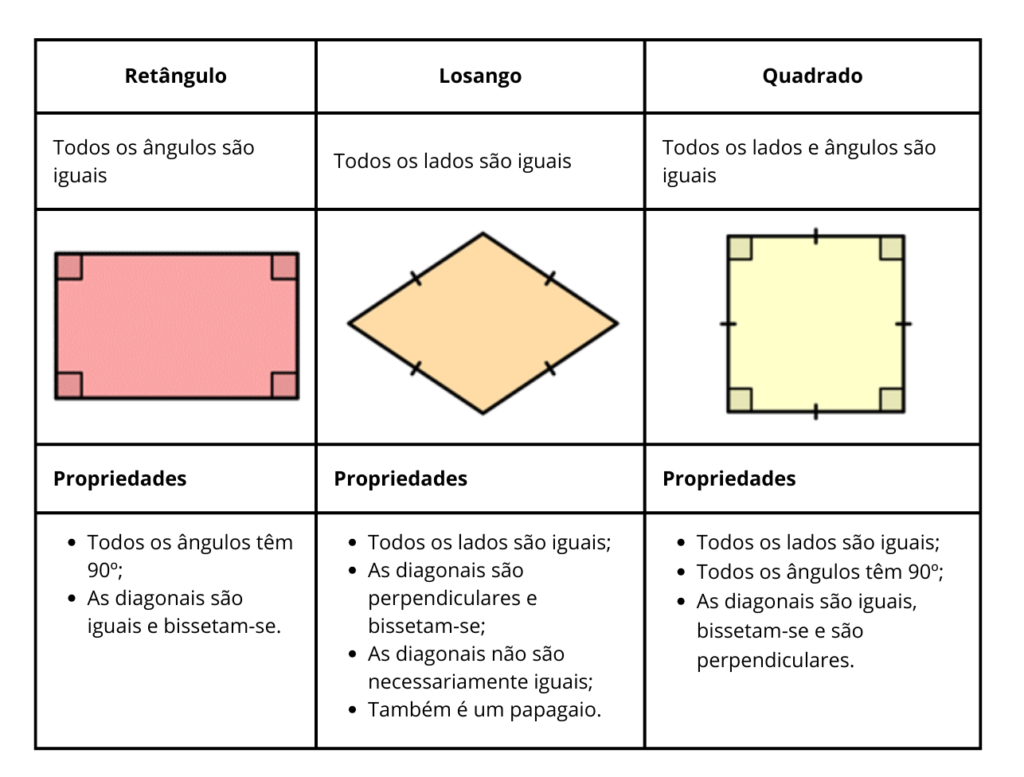
Tem apenas um par de lados paralelos. Este é o tipo mais comum de trapézio.
Os trapézios podem ser:

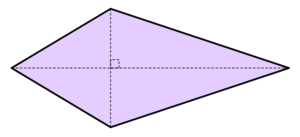
B. Papagaio
Um papagaio, também conhecido como deltoide, é um quadrilátero com dois pares de lados adjacentes iguais. As suas diagonais são perpendiculares.
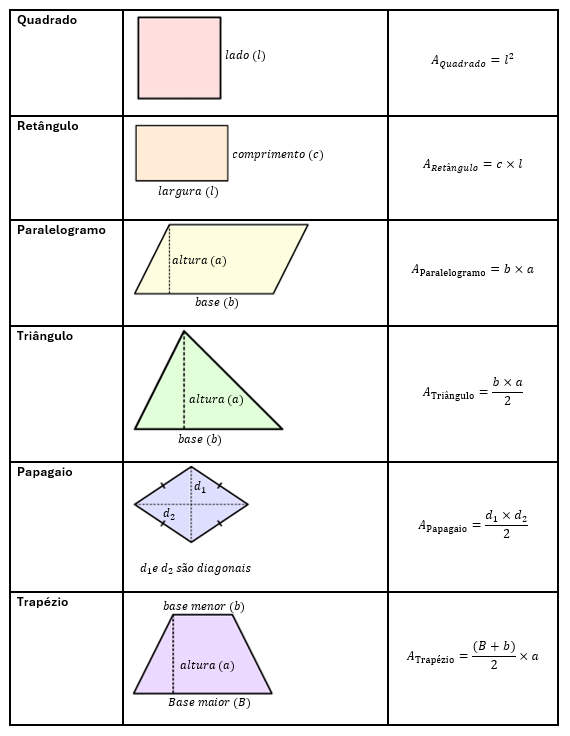
Calcular a área de figuras planas é uma habilidade fundamental em geometria, utilizada para determinar o espaço que uma figura cobre. Abaixo estão as fórmulas para calcular a área de algumas figuras geométricas planas comuns.